When you run prob += lpSum([x1, x3]) < 2, you get the following error:
Traceback (most recent call last): File "xyz.py", line 13, in
prob += lpSum([x1, x3]) < 2 TypeError: '<' not supported between instances of 'LpAffineExpression' and 'int'
This is the pulp package telling you that you cannot add strict inequalities, which is a standard requirement in optimization solvers. Since all your variables are binary valued, <2 is the same as <=1, and making this change will make the solver happy:
prob += lpSum([x1, x3]) <= 1
prob.solve()
print(x1.value(), x2.value(), x3.value(), x4.value())
# 0.0 1.0 1.0 0.0
So now you get a different solution with the same objective value of 3 (x2=1 and x3=1).
If you had wanted to output all possible solutions, you could use a loop to keep adding constraints disallowing the optimal solution until the optimal objective value changes:
from pulp import *
x1 = pulp.LpVariable('x1', cat=LpBinary)
x2 = pulp.LpVariable('x2', cat=LpBinary)
x3 = pulp.LpVariable('x3', cat=LpBinary)
x4 = pulp.LpVariable('x4', cat=LpBinary)
prob = pulp.LpProblem('x1+x2+2*x3+x4', pulp.LpMaximize)
prob += lpSum([x1, x2, 2*x3, x4])
prob += lpSum([x1, x2, x3, x4]) == 2
prob.solve()
print(x1.value(), x2.value(), x3.value(), x4.value())
opt = prob.objective.value()
while True:
prob += lpSum([x.value() * x for x in [x1, x2, x3, x4]]) <= 1 + 1e-6
prob.solve()
if prob.objective.value() >= opt - 1e-6:
print(x1.value(), x2.value(), x3.value(), x4.value())
else:
break # No more optimal solutions
This yields the expected output:
# 1.0 0.0 1.0 0.0
# 0.0 1.0 1.0 0.0
# 0.0 0.0 1.0 1.0
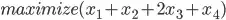
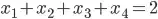
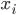 = {0,1} (binary variables).
= {0,1} (binary variables).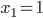 ,
, 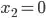 ,
, 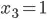 and
and  . However, I would like to disallow this solution, adding another constraint as
. However, I would like to disallow this solution, adding another constraint as 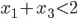 in Pulp as:
in Pulp as: