Why is A _< B always true in a Polynomial Reduction?

Question

I'm extremely knew to Computer Science, particularly the theoretical side, so am trying to understand (without an answer going too far over my head) why 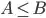is always true in a polynomial time reduction, and whether my naive theory as to why explains it (which I suspect doesn't).

My idea:

Premise: Starting off, I have two problems A and B, where either I'm finding A much more computationally expensive timewise to compute than B using the algorithm for A I have, or I haven't got an algorithm for A at all (making it very 'hard' indeed - though I hope I've used the term correctly here?). I realise though I can transform A into B and do just that.

When someone says that after such a reduction, a solution to A is always at most as hard as one for B, they don't mean that any algorithm that solves A is at most as hard as B, but in fact strictly that the most efficient that's currently known solution we will have for A from now on (which of course may be subject to change as we find better and better algorithms for a problem) will be at most, as hard as B or easier?

Why: Simply 3 cases - Firstly, if A was super hard to solve using the algorithm I had, but B was easier to solve and I used B to solve A, well now my most efficient solution to A is the algorithm for B. Secondly, if I had no solution to A at all but reduced A to B, well now I have 1 solution to A - so the 'union of all my solutions' is as hard as B's. Thirdly, say my best solution for A was always easier than B, but I 'reduced' it to B for fun, well my best solution is indeed easier than B.

There may be infinitely many more solutions to A that are harder than B (e.g. an algorithm that solves 2 + x = 4 straight away, vs one that does the same thing but for some reason adds 1 one million times to the equation, before subtracting it again, then solving).

Critically: So, since then there are any number of ways to solve a problem A that are arbitrarily more difficult than any particular solution, it only makes sense to talk of 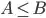in terms of the most efficient solutions to each that are currently known.

Is this right?

Thanks so much for your help, I really appreciate it.

Answer 1

Generally speaking, when people discuss "problems" and "how hard they are to solve", they are referring to the class of problem (e.g. the Traveling Salesman Problem) as opposed to a particular instance of the problem (e.g. the Traveling salesman problem with cities A, B, C... and distances X, Y, Z, ...). Further, when they discuss how hard/easy a problem is, they are referring to the most efficient possible solution. It's not very interesting to talk about how hard it is to solve a problem using a random solution (that might be really inefficient), so often solutions are accompanied proofs that there can be no solution more efficient.

So if the class of problem A can be transformed in to the class of problem B, then you know that there is a solution to A that is at least as efficient as B, since one solution is to transform it to B and solve it that way. It might be more efficient, since there may be a solution unique to problems of type A that is more efficient than those of type B, but it will be at least as efficient as B.

So your thinking is kind of in the right direction, but focus less on "solutions you happen to know about" and more about the theoretically most efficient solution to a problem.