3

I'm interested in creating an algorithm that provides a user ranking based on 3 actions that are weighted in significance. Example:

  • Action A (50%)
  • Action B (30%)
  • Action C (20%)

I would then like to have a time decay which provider maximum value at the time of the action and decays to 0 over a period like (day/week/month/year).

Any suggestions on where to start, how to go about implementing an algorithm like this?

Updates based on Jim's comments:

  • values of A,B,C are an aggregate number of points with equal value... the # of times a user performed the action
  • The time component should decay linearly. no acceleration.
user3386109
  • 34,287
  • 7
  • 49
  • 68
AnApprentice
  • 108,152
  • 195
  • 629
  • 1,012
  • 3
    Start by more clearly defining the requirements. What are the expected values of actions A, B, and C? Is it just a true/false flag that the user has performed those actions? Or is there some number of points multiplied by the number of times the user performed the action? With the time component, do you want it to decay linearly, or do you want it to fall off slowly at first and then accelerate? – Jim Mischel May 03 '18 at 17:12
  • @JimMischel sorry about the missing info. I just updated the question with the extra info. Thank you – AnApprentice May 03 '18 at 17:46
  • 2
    At least add some sample data to your question. {is there a timestamp, are the ABC events/counts present on every record?} – wildplasser May 03 '18 at 18:49

2 Answers2

2

Any suggestions on where to start

The obvious solution is to keep track of every event, along with a timestamp for that event. Then the rest is just math. However, that may require more storage, and more computation time than is desirable.

So my suggestion is to use binning. If the overall time decay period is one day, then use 12 two-hour bins. For example, at midnight the first bin (which represents the 00:00am to 02:00am time period) is cleared. Then any events that occur before 2:00am update the ABC counters in that bin. The bin has full weight until 2:00am, after which it is reduced in weight, until getting cleared again at midnight.

If the time period is a week, use 7 daily bins or 14 half-day bins. For a one month period, use 15 two-day bins, or 10 three-day bins. And for a year, use 12 monthly bins.

user3386109
  • 34,287
  • 7
  • 49
  • 68
  • Thank you, great idea with the bins. although performance won't be a concern for some time.... how do you recommend handling the time decay aspect? – AnApprentice May 03 '18 at 19:58
  • @AnApprentice With twelve bins, each bin has a weight from 12/12 down to 1/12. The current bin has weight 12/12, and the oldest bin has weight 1/12. So for example, if the current time is 08:32, then the 08:00-10:00 bin has weight 12/12, the 06:00-08:00 bin has weight 11/12, etc. – user3386109 May 03 '18 at 20:21
2

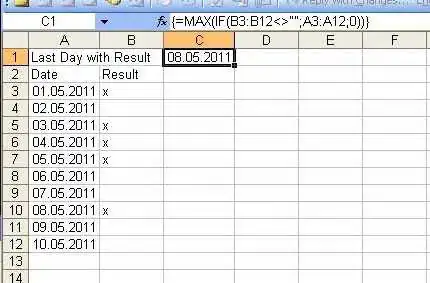
Taking a shot at giving a high level design.

There are only two reasons why a user's score will change:

  1. The user performed some action; or,
  2. A unit of time passed.

The time's interaction results in a linear decay†.

The Algorithm

You are trying to rank users, on the basis of score generated from their contribution to the Actions A, B, and C. Let's start with outlining what the software will do when one of the two causes for score change occurs.

  1. When a user performs an action: Generate the user's scores for the rest of time assuming that user will commit no further action and put them in a queue within the user object. The front of the queue will tell the current score of the user.

  2. When a unit of time passes: Just dequeue the front from its score queue.

The Data Structures

It seems to me that the traditional data structures - Arrays, Trees, Hashmaps - and even the usual augmented data structures - Linked Hashmap, Red Black Tree - will not be sufficient to calculate rank for such a scoring model. You will need to move a level up to get the right data structure for generating rank from this scoring system.

I can imagine a multi-doubly-linked kind of Hashmap. Would look somewhat like this:

Multi-augmented Data Structure

So in the diagram above, we have one common storage containing all the user objects. Then we have multiple singly/doubly linked indices into the user storage. This way all the indices associated with the user object will be updatable, when user's score changes.

Finally, the ranking can be allowed to not necessarily begin from 1. The sorted-concurrent-hashmap can be updated and could hold negative ranks. Since the map is sorted, the most negative rank will be the first rank and further ranks can be obtained by sorted map's traversal. The ranks can be normalized back to start with some high positive number when the minimum rank gets close to the underflow limit.

This is a pretty big problem. There are many more ideas and optimizations that I have in mind. It is too big a task to mention all of them here. If you have a specific question, I can try to answer that.

†The time's interaction results in a linear decay. So I assume that the calculating the time decaying score from user's current score to next (let's say) 100 scores is simple. How many future scores need to be calculated will depend on what you consider to be one unit of time.

displayName
  • 13,888
  • 8
  • 60
  • 75