Basically, I have two matrices A and B, and I want C (dimensions marked by the side of the matrices), with computation like this:
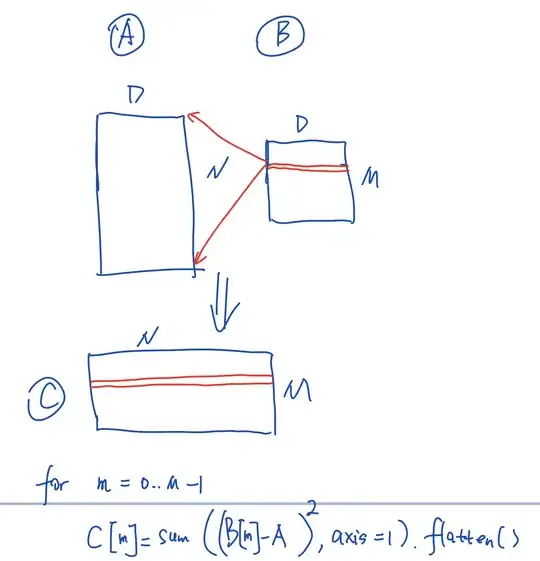
The formula below is what I do now. I take advantage of some broadcasting, but I am still left with a loop. I am novel to Python so maybe I am wrong, but I just have a hunch that this loop can be eliminated. Can anyone share some ideas?
EDIT: 2018-04-27 09:48:28 as requested, an example:
In [5]: A
Out[5]:
array([[0, 1],
[2, 3],
[4, 5],
[6, 7],
[8, 9]])
In [6]: B
Out[6]:
array([[0, 1],
[2, 3],
[4, 5],
[6, 7]])
In [7]: C = np.zeros ((B.shape[0], A.shape[0]))
In [8]: for m in range (B.shape[0]):
...: C[m] = np.sum (np.square (B[m] - A), axis=1).flatten ()
...:
In [9]: C
Out[9]:
array([[ 0., 8., 32., 72., 128.],
[ 8., 0., 8., 32., 72.],
[ 32., 8., 0., 8., 32.],
[ 72., 32., 8., 0., 8.]])