Random point in Miller's Weil Pairing algorithm

Question

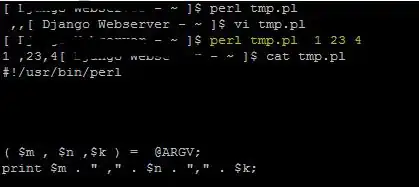
I'm trying to implement the Miller's Weil Pairing algorithm but I have a problem.
I used the book "An introduction to mathematical cryptography" by Hoffstein, Pipher and Silverman and tried my implementation with the example given in the book :

I obtain the same response so the computations should be good but I have a problem choosing a random point S. In the book, it is stated that we must choose a point S not in {O,P,-Q,P-Q}.
But with this equation :

I try to compute e(P,Q) with P = (1,5) and Q = (12,2) of order 9 but there is always an error at one moment because the result of the Miller's function is 0/0. -Q = (12,11) and P-Q = (9,6) so I tried with all the others points and it does not work with points of the same order which is normal. (9,6) and (9,7) are the only ones that have a different order : 3. As (9,6) cannot be chosen I took (9,7) but I still get some 0 that create problems.
Can someone tell me what I did wrong or what I didn't understood ?
Thank you

Here is the code :

def g(p, q, r, curve):

modulo = curve.p
if p.x is None and p.y is None:
    return (r.x - q.x) % modulo
if q.x is None and q.y is None:
    return (r.x - p.x) % modulo
if p != q and p.x == q.x:
    return (r.x - p.x) % modulo

l = slope(p, q, curve)
num = (r.y - p.y - l*(r.x - p.x)) % modulo
denom = (r.x + p.x + q.x - l**2) % modulo

return (num * mult_inverse(denom, modulo)) % modulo


def miller_algorithm(p, q, m, curve):

f = 1
t = copy(p)

n = list(bin(m)[2:])
for i in range(1,len(n)):
    f = (f**2) * g(t, t, q, curve)
    t = t.double_and_add(2)
    if n[i] == '1':
        f = f * g(t, p, q, curve)
        t = t.add(p)
return f % curve.p


def weil_pairing(p, q, curve):

if p == q or (p.x is None and p.y is None) or (q.x is None and q.y is None):
    return 1
m = q.order()

s = curve.random_point()
while s == p or s == q.neg() or s == (p.sub(q)) or s.order() == m:
    s = curve.random_point()

fpnum = miller_algorithm(p, q.add(s), m, curve)
fpdenom = miller_algorithm(p, s, m, curve)
fqnum = miller_algorithm(q, p.sub(s), m, curve)
fqdenom = miller_algorithm(q, s.neg(), m, curve)

modulo = curve.p
num = (fpnum * mult_inverse(fpdenom, modulo)) % modulo
denom = (fqnum * mult_inverse(fqdenom, modulo)) % modulo
return (num * mult_inverse(denom, modulo)) % modulo

http://tpcg.io/GZNfns The first example gives the correct final response which is 242. The complete image of the first example is here : https://imgur.com/a/x5JHM But for the 2nd, I obtain two 0 which can't happen normally. So I thought that the problem came from the point S but even if I test with all the possible points there is always some 0 at some point. — user1241025, Apr 17 '18 at 14:36
Despite the fact that there's some code involved I think this would be a much better fit on [Math exchange](http://math.stackexchange.com) — President James K. Polk, Apr 17 '18 at 21:09

score 1 · Answer 1 · answered Apr 13 '22 at 16:23

I can't tell you what you are doing incorrectly. But, the python program sagemath has an implementation of miller's algorithm, and all the pairings, weil, tate, and ate. If you install it, you can find the source code for miller and weil in the file ell_point.py. The algorithm is more general, and so more complex, than your implementation, but you should be able to translate to get what you want. Or, you can just import sagemath and use its implementations.

Random point in Miller's Weil Pairing algorithm

1 Answers1