3

I'm working through some exercises on improper integrals and I've stumbled across an issue I can't resolve. I'm attempting to use the limit() function on the following problem:

Question

Here N(x) is the cumulative distribution function of the standard normal variable.

Cumulative distribution function

The limit() function so far hasn't caused any problems, including problems which require L'Hôpital's rule be applied. However, I'm struggling to get compute the correct answer for this particular problem and can't work out why. The following code yields an incorrect answer

Incorrect solution

from sympy import *

x, y = symbols('x y')
init_printing(use_unicode=False) #Print the answers in unicode characters

cum_distribution = (1/sqrt(2*pi)*(integrate(exp(-y**2/2), (y, -oo, x))))

func = (cum_distribution -(1/2)-(x/sqrt(2*pi)))/(x**3)

limit(func, x, 0)

If I apply L'Hôpital's rule, i get the correct

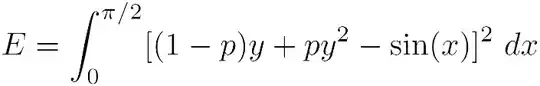
Correct solution

l_hopital = diff((cum_distribution -(1/2)-(x/sqrt(2*pi))), x)/diff(x**3, x)

limit(l_hopital, x, 0)

I looked through the limit() function source code and my understanding is that L'Hôpital's rule isn't applied? In this case, can this problem be solved using the limit() function without applying this rule?

Josmoor98
  • 1,721
  • 10
  • 27

1 Answers1

3

At present, a limit involving the function erf (known as the error function, related to normal CDF) can only be evaluated when the argument of erf tends to positive infinity. Limits at other places are either not evaluated, or evaluated incorrectly. (Related PR). This includes the limit

limit(-(sqrt(2)*x - sqrt(pi)*erf(sqrt(2)*x/2))/(2*sqrt(pi)*x**3), x, 0)

which returns unevaluated (though I would not call this incorrect). As a workaround, you can compute the Taylor series of this function with one term (the constant term), which gives the correct value of the limit:

series(func, x, 0, 1).removeO()

returns -sqrt(2)/(12*sqrt(pi)).

As in calculus practice, L'Hopital's rule is inferior to power series techniques when it comes to algorithmic computations, and SymPy relies primarily on the latter. The algorithm it uses is devised and explained in On Computing Limits in a Symbolic Manipulation System by Dominik Gruntz.

Josmoor98
  • 1,721
  • 10
  • 27