Use numpy to solve transport equation with wave-like initial condition

Question

I'm trying to write a python program to solve the first order 1-D wave equation (transport equation) using the explicit Euler method with 2nd order spatial discretization and periodic boundary conditions.

I'm new to python and I wrote this program using numpy but I think I'm making a mistake somewhere because the wave gets distorted. Instead of the wave simply translating to the left it seems to get distorted once it leaves the left boundary. I'm pretty sure this is a programming error but is it possible it's a rounding error? Am I not using numpy correctly? Any advice on writing this program in a more python-esque way? Thanks!

The PDE is

in finite difference form it is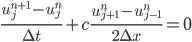

solving for

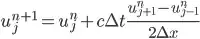
Here is what I attempted:

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation

# wave speed
c = 1

# spatial domain
xmin = 0
xmax = 1

n = 50 # num of grid points

# x grid of n points
X, dx = np.linspace(xmin,xmax,n,retstep=True)

# for CFL of 0.1
dt = 0.1*dx/c

# initial conditions
def initial_u(x):
    return np.exp(-0.5*np.power(((x-0.5)/0.08), 2))

# each value of the U array contains the solution for all x values at each timestep
U = []

# explicit euler solution
def u(x, t):
    if t == 0: # initial condition
        return initial_u(x)
    uvals = [] # u values for this time step
    for j in range(len(x)):
        if j == 0: # left boundary
            uvals.append(U[t-1][j] + c*dt/(2*dx)*(U[t-1][j+1]-U[t-1][n-1]))
        elif j == n-1: # right boundary
            uvals.append(U[t-1][j] + c*dt/(2*dx)*(U[t-1][0]-U[t-1][j-1]))
        else:
            uvals.append(U[t-1][j] + c*dt/(2*dx)*(U[t-1][j+1]-U[t-1][j-1]))
    return uvals

# solve for 500 time steps
for t in range(500):
    U.append(u(X, t))

# plot solution
plt.style.use('dark_background')
fig = plt.figure()
ax1 = fig.add_subplot(1,1,1)

# animate the time data
k = 0
def animate(i):
    global k
    x = U[k]
    k += 1
    ax1.clear()
    plt.plot(X,x,color='cyan')
    plt.grid(True)
    plt.ylim([-2,2])
    plt.xlim([0,1])

anim = animation.FuncAnimation(fig,animate,frames=360,interval=20)
plt.show()

this is how the wave starts

and this is how it ends up after a few iterations

Can anyone please explain why this (the wave distortion) is happening?

Answer 1

Your implementation is correct. The distortion comes from relatively large spatial step dx. At its current value of 0.2 it is comparable to the size of the wave, which makes the wave visibly polygonal on the graph. These these discretization errors accumulate over 500 steps. This is what I get from plt.plot(X, U[-1]) with your code:

And this is what I get after using n = 100 (halving both time and space stepsize), running the solution for t in range(1000) to compensate for smaller time step, and again plotting plt.plot(X, U[-1]):

The symmetric-difference approximation for du/dx has error of order dx**3 proportional to the third derivative. The manner in which these accumulate is complicated because the solution is moving around, but in any case smaller dx improves the matters if dt scales with it.