4 year old thread, but I happened to stumble accross it when googling my problem.
I have a problem like this in a current CV application. I came up with a simple and somewhat clumsy solution for the finding the largest. Not exactly the same though, cause I maximize the area of the rectangle without a fixed ratio of sides.
I don't know yet wether my solutions finds the optimum or whether it works in all cases. I also think there should be a more efficient way, so I am looking forward to your input.
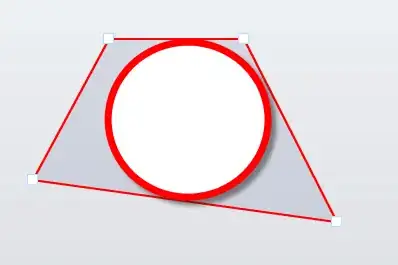
First, assume a set of 4 points forming our (convex) quadrilateral:
x y
P1 -2 -5
P2 1 7
P3 4 5
P4 3 -2
For this procedure the leftmost point is P1, the following points are numbered clockwise. It looks like this:

We then create the linear functions between the Points. For each function we have to know the slope k and the distance from 0: d.
k is simply the difference in Y of the two points divided by the difference in X.
d can be calculated by solving the linear function to d. So we have
k=dy/dx
d=y1-k*x1
We will also want the inverse functions.
k_inv = 1/k
d_inv = -d/k
We then create the function and inverse function for each side of the quadrilateral
k d k d
p1p2 4 3 p1p2_inv 0.25 -0.75
p2p3 -0.67 7.67 p2p3_inv -1.5 11.5
p3p4 7 -23 p3p4_inv 0.14 3.29
p4p1 0.6 -3.8 p4p1_inv 1.67 6.33
If we had completely horizontal or vertical lines we would end up with a DIV/0 in one of the functions or inverse functions, thus we would need to handle this case separately.
Now we go through all corners that are enclosed by two functions that have a k with a slope with a different sign. In our case that would be P2 and P3.
We start at P2 and iterate through the y values between P2 and the higher one of P1 and P3 with an appropriate step size and use the inverse functions to calculate the distance between the functions in horizontal direction. This would give us one side of the rectangle
a=p2p3_inv(y)-p1p2_inv(y)
At the two x values x = p2p3_inv(y) and x = p1p2_inv(y) we then calculate the difference in y to the two opposite functions and take the distance to our current y position as a candidate for the second side of our rectangle.
b_candidate_1 = y-p4p1(p2p3_inv(y))
b_candidate_2 = y-p4p1(p1p2_inv(y))
b_candidate_3 = y-P3p4(p2p3_inv(y))
b_candidate_4 = y-P3p4(p1p2_inv(y))
The lesser of the four parameters would be the solution for side b.
The area obviously becomes a*b.
I did a quick example in excel to demonstrate:
the minimum b here is 6.9, so the upper right corner of the solution is on p2p3 and the rectangle extends a in horizontal and b in vertical direction to the left and bottom respectively.
The four points of the rectangle are thus
Rect x y
R1 0.65 -1.3
R2 0.65 5.6
R3 3.1 5.6
R4 3.1 -1.3

I will have to put this into C++ code and will run a few tests to see if the solution generalizes or if this was just "luck".
I think it should also be possible to substitute a and b in A=a*b by the functions and put it into one linear formula that has to be maximized under the condition that p1p2 is only defined between P1 and P2 etc...