Solve nonlinear equation in python

Question

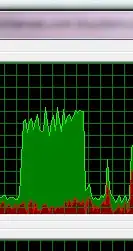
I am trying to find the fundamental TE mode of the dielectric waveguide. The way I try to solve it is to compute two function and try to find their intersection on graph. However, I am having trouble get the intersect point on the plot. My code:

def LHS(w):
    theta = 2*np.pi*1.455*10*10**(-6)*np.cos(np.deg2rad(w))/(900*10**(-9))
    if(theta>(np.pi/2) or theta < 0):
        y1 = 0
    else:
        y1 = np.tan(theta)
    return y1

def RHS(w):
    y = ((np.sin(np.deg2rad(w)))**2-(1.440/1.455)**2)**0.5/np.cos(np.deg2rad(w))
    return y

x = np.linspace(80, 90, 500)

LHS_vals = [LHS(v) for v in x]
RHS_vals = [RHS(v) for v in x]


# plot
fig, ax = plt.subplots(1, 1, figsize=(6,3))
ax.plot(x,LHS_vals)
ax.plot(x,RHS_vals)
ax.legend(['LHS','RHS'],loc='center left', bbox_to_anchor=(1, 0.5))

plt.ylim(0,20)
plt.xlabel('degree')
plt.ylabel('magnitude')
plt.show()

I got plot like this:

The intersect point is around 89 degree, however, I am having trouble to compute the exact value of x. I have tried fsolve, solve to find the solution but still in vain. It seems not able to print out solution if it is not the only solution. Is it possible to only find solution that x is in certain range? Could someone give me any suggestion here? Thanks!

edit: the equation is like this (m=0):

and I am trying to solve theta here by finding the intersection point

edit: One of the way I tried is as this:

from scipy.optimize import fsolve
def f(wy):
   w, y = wy
   z = np.array([y - LHS(w), y - RHS(w)])
   return z

fsolve(f,[85, 90])

However it gives me the wrong answer. I also tried something like this:

import matplotlib.pyplot as plt

x = np.arange(85, 90, 0.1)
f = LHS(x)
g = RHS(x)

plt.plot(x, f, '-')
plt.plot(x, g, '-')

idx = np.argwhere(np.diff(np.sign(f - g)) != 0).reshape(-1) + 0
plt.plot(x[idx], f[idx], 'ro')
print(x[idx])
plt.show()

But it shows: ValueError: The truth value of an array with more than one element is ambiguous. Use a.any() or a.all()

Can you post the equation you're trying to solve? Also, how are you looking for an intersection? — Alex Dubrovsky, Feb 12 '18 at 13:20
Make sure to tag the question according to the *actual* problem and to show the code of the *actual* problem. There is no attempt to use `fsolve` or anything similar in the question. (On the other hand the problem is completely unrelated to matplotlib.) — ImportanceOfBeingErnest, Feb 12 '18 at 13:29
First, your LHS is a discontinuous function, `fsolve` assumes a smooth argument. Second, your RHS is different from what you show on your plot. Third, your RHS is not a real function, i.e. the argument of `sqrt(x)` becomes negative when `w` approaches the value of 82. — Dima Chubarov, Feb 12 '18 at 13:58
General remark from my experience with nonlinear equations - investigate the equation thoroughly before solving it numerically, especially for functions with discontinuities and things like negative arguments of `sqrt(x)`. — Alex Dubrovsky, Feb 12 '18 at 16:49

score 3 · Answer 1 · answered Feb 13 '18 at 14:02

First, you need to make sure that the function can actually handle numpy arrays. Several options for defining piecewise functions are shown in Plot Discrete Distribution using np.linspace(). E.g.

def LHS(w):
    theta = 2*np.pi*1.455*10e-6*np.cos(np.deg2rad(w))/(900e-9)
    y1 = np.select([theta < 0, theta <= np.pi/2, theta>np.pi/2], [np.nan, np.tan(theta), np.nan])
    return y1

This already allows to use the second approach, plotting a point at the index which is closest to the minimum of the difference between the two curves.

import numpy as np
import matplotlib.pyplot as plt

def LHS(w):
    theta = 2*np.pi*1.455*10e-6*np.cos(np.deg2rad(w))/(900e-9)
    y1 = np.select([theta < 0, theta <= np.pi/2, theta>np.pi/2], [np.nan, np.tan(theta), np.nan])
    return y1

def RHS(w):
    y = ((np.sin(np.deg2rad(w)))**2-(1.440/1.455)**2)**0.5/np.cos(np.deg2rad(w))
    return y

x = np.linspace(82.1, 89.8, 5000)
f = LHS(x)
g = RHS(x)

plt.plot(x, f, '-')
plt.plot(x, g, '-')

idx = np.argwhere(np.diff(np.sign(f - g)) != 0).reshape(-1) + 0
plt.plot(x[idx], f[idx], 'ro')
plt.ylim(0,40)
plt.show()

One may then also use scipy.optimize.fsolve to get the actual solution.

idx = np.argwhere(np.diff(np.sign(f - g)) != 0)[-1]

from scipy.optimize import fsolve

h = lambda x: LHS(x)-RHS(x)
sol = fsolve(h,x[idx])

plt.plot(sol, LHS(sol), 'ro')
plt.ylim(0,40)
plt.show()

Alex Dubrovsky · Accepted Answer · 2018-02-12T17:06:44.680

Something quick and (very) dirty that seems to work (at least it gave theta value of ~89 for your parameters) - add the following to your code before the figure, after RHS_vals = [RHS(v) for v in x] line:

# build a list of differences between the values of RHS and LHS
diff = [abs(r_val- l_val) for r_val, l_val in zip(RHS_vals, LHS_vals)]

# find the minimum of absolute values of the differences
# find the index of this minimum difference, then find at which angle it occured
min_diff = min(diff)
print "Minimum difference {}".format(min_diff)
print "Theta = {}".format(x[diff.index(min_diff)])

I looked in range of 85-90:

x = np.linspace(85, 90, 500)

Solve nonlinear equation in python

2 Answers2