I have been given a strictly convex polygon of S sides and Q queries to process.
All points of polygon and query points are given in (x,y) pairs.The points of the polygon are given in anti-clockwise order.
The aforementioned variables are limited such that 1<=S<=10^6 and 1<=Q<=10^5 and 1<=|x|,|y|<=10^9.
For each query I should output Yes if the given point lies inside the polygon; otherwise, No.
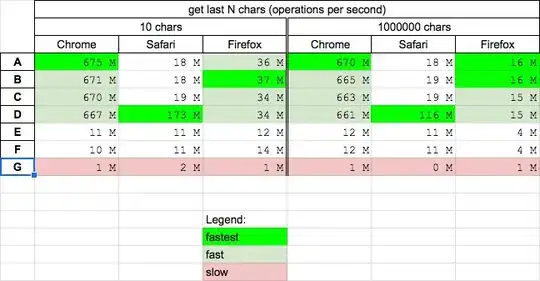
I tried using an O(S) inclusion test (ray-casting) and it timed out for the bigger test cases but also didn't pass all the preliminary ones.
Obviously, the implementation didn't cover all the edge cases and I got to know about a specific algorithm for this question which could answer each query in O(log S) using binary search but I can't figure out how to implement it from the pseudocode (first time doing computational geometry).
Could anyone provide me with the algorithm which covers all edge cases within the required time complexity (Q log S) or guide me to a page or paper that implements it?