I'm coming from biology's field and thus I have some difficulties in understanding (intuitively?) some of the ideas of that paper. I really tried my best to decipher it step by step by using a lot of google and youtube, but now I feel, it's the time to refer to the professionals in that field.
Before filling out the whole universe with (unordered) questions, let me put the whole thing down and try to introduce you to the subject while at the same time explain to you what I got so far from my research on that.
Microarrays
For those that do not have any idea of what this is, you can imagine, that it is literally an array (matrix) where each cell of it contains a probe for a specific gene. Making the long story short, by the end of the microarray experiment, you have a matrix (in computational terms) with each column representing a sample, each line a different gene while the contents of the matrix represent the expression values of the genes for each sample.
Pathways
In biology pathway / gene-set they call a set of genes that interact with each other forming a small network responsible for a specific function.These pathways are not isolated but they talk/interact with each other too. What that paper does on the first hand, is to expand the initial pathway (let us call it target pathway), by including some other genes from other pathways that might interact with that.
Procedure
1.
Let's assume now that we have a matrix G x S. Where G for genes and S for Samples. We construct a gene co-expression network (G x G) using as weights the Pearson's correlation coefficients between genes' pairs (a). This could also be represented as an undirected weighted graph.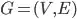 
.
2. For each gene (row OR column) we calculate the weighted degree (d) which is nothing more than the sum of all correlation coefficients of that gene.
3. From the two previous matrices, they construct the transition matrix producing the probabilities (P) to transit from one gene to another by using the
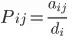formula
Q1. Why do they call this transition probability? Is there any intuitive way to see this as a probability in the biological context?
4. Since we have the whole transition matrix, we can define a subnetwork of the initial one, that we want to expand it and it consisted out of let's say 15 genes. In that step, they used formula number 3 (on the paper) which transforms the values of the initial transition matrix as it says. They set the probability of 1 on the nodes that are part of the selected subnetwork because they define them as absorbing states.
Q2. In that same formula (3), I cannot understand what the second condition does. 
When should the probability be 0? Intuitively, in my opinion, all nodes that didn't exist in subnetwork, should have the P_ij value as a probability.
5. After that, the newly constructed transition matrix is showed at formula (4) in the paper and I managed to understand it using this excellent article.
6. Here is where everything is getting more blur for me and where I need the most of the help. What I imagine at that step, is that the algorithm starts randomly from one node and keep walking around the network. In order to construct a relevance function (What that exactly means?), they firstly calculate a probability called joint probability of visiting one node/edge E(i,j) and noted as :
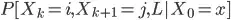
From the other hand they seem to calculate another probability called probability of a walk of length L starting in x and denoted as :
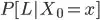
7. In the next step, they divide the previously calculated probabilities and calculate the number of times a random walk starts in x using the transition from i to j that I don't really understand what this means.
After that step, I lost their reasoning at all :-P.
I'm not expecting an expert to come open my mind and give me understand that procedure. What I'm expecting is some guidelines, hints, ideas, useful resources or more intuitive approaches to understanding the whole procedure. Then when I fully understand it I will try to implement it on R or python.
So any idea / critics is welcome.
Thanks.
