1

I am trying to implement frustum culling in my OpenGL 2d game. The only kind of geometric objects in my game at this point are rectangles, so I thought this would be pretty easy, but I am getting unexpected results. I have setup a symmetrical perspective projection with a field-of-view angle of 45 degrees, and near and far planes at 0.01 and 50 respectively. The eye vector is always parallel to the z-axis, the camera can only move along the x and y axes.

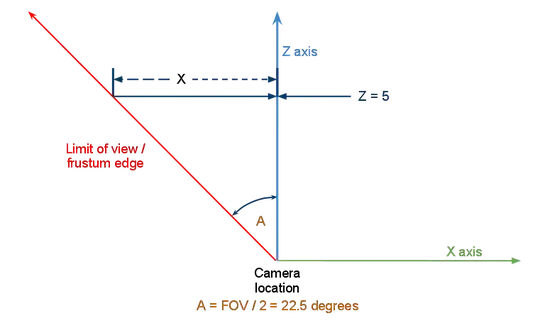
My idea was to get the rectangular area of the world space that is currently visible to the camera at the z-coordinate of the rectangle I am trying to cull. Because the camera is looking at the center of the frustum, I calculate the distance to the edges of this visible rectangular area as follows: 

GLfloat maxDistance = givenRectangle.z * tanf(0.5 * (fovAngle * M_PI/180) );

Then I add and substract this distance to and from the x and y coordinates of the camera to get the maximum and minimum visible x and y, and then test the given rectangle to see if it's in between these values.

My question is whether I am on the right track here, and why the above formula returns an absurdly small value (something*10^-37) when I have an object at z=5, which should clearly be visible with the Camera at (0,0,0)?

Jacob
  • 23
  • 5
  • Yeah well technically I only have 2d rectangles in a 3d perspective so, whatever you'd like to call that :) The reason I want the perspective projection is that I want to be able to zoom in and out, I have a world with a topdown camera orientation – Jacob Jan 31 '11 at 11:44
  • could you explain me that part please : Then I add and substract this distance to and from the x and y coordinates of the camera to get the maximum and minimum visible x and y, and then test the given rectangle to see if it's in between these values. – jocelyn Jan 22 '13 at 20:28

1 Answers1

3

Taking the problem from the top, I've checked your formula - see sketch to confirm I've understood you correctly.

enter image description here

Given that we know A and Z and want to solve for X, I first wrote:

tan(A) = X/Z

rearranging, I get:

X = Z tan(A)

Since Z = 5 and A = 22.5 degrees...

X = 5* tan(22.5 degrees)

X = 2.07106781

So, it does seem as though you've got the maths right but your code wrong - maybe your tan function is expecting degrees rather than radians, or fovAngle hasn't been set? I think you need to debug and hand-check each value.

Going back to the wider problem of figuring out what does and does not lie inside your frustum, you might find that you can use a different test to answer the same question more elegantly. Many graphics coders use a "side-of-plane" test. Consider that your viewing frustum is a volume of space bounded by a set of 6 planes (4 for the sides of your viewport, a near clipping plane and a far clipping plane).

Given a point on a plane and a normal for the plane, you can quite easily calculate the equation of a plane, which in turn makes it trivial to test whether a given point is "inside" (in the direction of the normal) a given plane. Iterate through all 6 planes and you'll quickly rule a given point in or out of your viewing volume.

The really neat thing about this test is how easily you can re-use it: any simple convex polygon you happen to want to do tests on (e.g. a rectangle) can be described as a set of planes, allowing you to re-use your "insider or outside" test. Very general.

Edward Dixon
  • 591
  • 4
  • 16
  • Thank you for your answer, this is indeed what I meant. I also found out what the problem was: it was something with a double pointer to fovAngle that wasn't working properly in my specific code...One question about your way of frustum culling: am I right in suspecting that this more general approach is slower for simple rectangles than the method I described? – Jacob Mar 06 '11 at 15:22
  • Glad you found the bug, sounds like a frustrating one. Yes, the planes method is sure to be slower. It could save you in development effort at some stage, but with your particular situation it might be overkill. – Edward Dixon Mar 07 '11 at 13:45
  • Speaking of speed, if you are writing a 2D game anyhow and really want to go all-out for performance, consider not using perspective. If you use an orthographic projection instead, your test for "is rectangle inside screen" will be simpler again, 0 < x < screen_width. – Edward Dixon Mar 07 '11 at 14:02
  • If you wan to be able to zoom out of the scene and see if object are visible or not you need this technique, even in 2d ! – jocelyn Jan 22 '13 at 19:58