Get the expectation of random variables function's distribution by sampling from the joint distribution

Question

I am not professional in Probability & Statisticsin, in order to clearly describe my problem, please be patient of the long introduction.THANKS!

Background of my question

Assume I have several independent random variables, say X and Y, and their distributions are already known, for example: X~N(0,1)$ and $y~N(0,1)$. Now there is a random function of X and Y, $$g(X,Y)=X^2+Y^2$$, g(X,Y) is a random variable too, make Z=g(X,Y), the distribution of g(X,Y) is unknown, mark it as . My goal is to get the expectation of g()'s distribution which is E[Z].

Here, the g(X,Y) has a easy form, I can tell g(X,Y) 's distribution is chi2(2). But when the form of g() is more complex, I can't get the distribution of g() directly, more difficult to get the expectation by g(X,Y)'s distribution. --BUT--, I found a web page on wiki which talking about "Law of the unconscious statistician". Then I realized I can get the expection of g()'s distribution by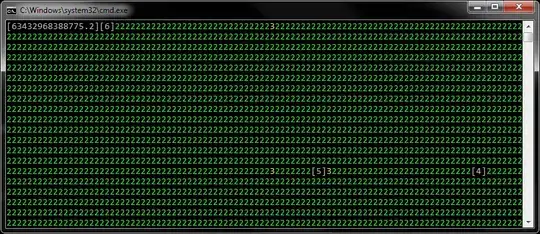:, here in this example, the joint distribution: and .

For the equation of E[Z], I think the MC(Monte Carlo) method is a suitable way to deal with it. I rewite the equation based on importance sampling:

h(x,y) is the proposal distribution which has know form. This is a great form to use Metropolis-Hasting Method.

What I want to test is: the expectation calculated by samples from chi2(2) distribution should be equal to the expectation calculated by MC method. I implement all above in python as shown blew:

import numpy as np
import time
import matplotlib.pyplot as plt
import numpy as np
import scipy.stats as st
from scipy.stats import chi2
%matplotlib inline
# np.random.seed(123)

def sampler(mean=[0,0], cov=[[1,0],[0,1]], n=10):
    return st.multivariate_normal(mean, cov).rvs(n) 

def g(point):
    return point[0]**2+point[1]**2
k=2
samples_from_chi2 = chi2.rvs(k,loc=0, scale=1, size=400)
mean_chi2 = np.mean(samples_from_chi2)

iterN = 10000
begin = np.array([2**.5, 2**.5])
samples = np.array(begin)
mulN_mean = np.array([0,0])
mulN_cov = np.array([[1,0],[0,1]])
multiNormal = st.multivariate_normal
p = multiNormal(mulN_mean, mulN_cov)
timeTest_begin = time.clock()
for i in range(iterN):
    #print("------------round{a:2d}---------------".format(a=i))
    father = begin
    pdf_father = p.pdf(father)
    son = multiNormal(father, mulN_cov).rvs(1)
    pdf_son = p.pdf(son)
    # print("father={a:%f}, son={b:%f}".format(a=father, b=son))

    ''' 
    in this example, P(father|son) == P(son|father) is true,
    so just ignore the conditional probability of Metropolis–Hastings 
    algorithm
    '''
    # q_son_father = multiNormal(father, mulN_cov).pdf(son)
    # q_father_son = multiNormal(son, mulN_cov).pdf(father)
    # print("q(son|father)=", q_son_father)
    # print("q(father|son)=", q_father_son)

    g_father = g(father)
    g_son = g(son)

    r_up = g_son * pdf_son
    r_down = g_father * pdf_father
    r = r_up / r_down
    u = np.random.rand()

    if r >= u:
        samples = np.vstack((samples, son))
    else:
        samples = np.vstack((samples, father))

    begin = samples[-1]

timeTest_end = time.clock()
T = timeTest_end - timeTest_begin
#print("cost time:%d\n", T)
# print("samples=\n", samples)

G_samples = samples[:,0]**2 + samples[:,1]**2
mean_from_sample = np.mean(G_samples)
print("chi2 mean:{a}    sample_mean:{b}".format(a=mean_chi2, 
b=mean_from_sample))

x = range(iterN+1)
y_max = np.max(G_samples)
y = np.linspace(0, y_max, int(y_max*40))
fig, (ax1, ax2) = plt.subplots(2,1)
ax1.plot(x,G_samples,'-')
ax1.set_title('Trace plot')
ax1.set_xlabel('Number of points')
ax1.set_ylabel('Points location')
ax2.hist(G_samples, int(iterN/100),normed=1)
ax2.set_title('Histogram plot')
ax2.set_xlabel('Points location')
ax2.set_ylabel('Probability')
ax2.plot(y,st.chi2.pdf(2, y), 'r')
fig.subplots_adjust(left=None, bottom=None, right=None, top=None,
            wspace=None, hspace=0.8)

The result of the implementation:

chi2 mean:2.0085551240837773    sample_mean:4.069302525056825

Here my question comes

No matter the number of sample points is 400 or 10000, the mean of the samples directly from chi-square distribution is about 2 (I confirm it is right, because if the freedom of chi2 distribution is k, then the expectation is k, and the variance is 2k), but the expectation calculated by MC method is about 4, just as shown above, I want to know why there is a 2 times relationship between two results, if the const's exist is right, how to find it's value when I don't know the random variable function's distribution(in this example, chi-square distribution)

Thanks for reading here, please give me some advice, thank you very much!

Update

the problem has been solved. My assumption has been confirmed: the result by tow ways are equal, and the M-H sampling way is more faster. Here is the new picture of the M-H way(the red line is the pdf plot of $\chi^2(2)$), and mean values of the expectation calculated by tow ways.

chi2 mean:2.0159110138904883    sample_mean:1.9693578501381137

Fine question. Wrong StackExchange site. – Gordon Linoff Jan 28 '18 at 12:53 — Gordon Linoff, Jan 28 '18 at 12:53

score 0 · Answer 1 · answered Feb 04 '18 at 13:40

You're right, the expectation value must be the same, so we must assume that there should be something wrong somewhere in the code. Going through it I found some steps I did not understand (maybe I'm wrong but I'm trying to understand how you implemented the MC)

First:

father = begin
pdf_father = p.pdf(father)
son = multiNormal(father, mulN_cov).rvs(1)
pdf_son = p.pdf(son)

Here you set each time father to the begin, but to construct a chain you have to update it if the move is accepted, i.e. goes to son. Then, the construction of the variable son starting from the father, but giving the argument 1 to the rvs method. Isn't this shifting the mean to 1?

Second. At the end, correctly, there is the Metropolis accept-reject step

if r >= u:
    samples = np.vstack((samples, son))
else:
    samples = np.vstack((samples, father))

but where does u is initialized? It must be picked from a uniform distribution in the range [0,1], but I don't find it in the code.

Putting together these doubts (if I am correct) a possible answer could be the following: the son variable is defined from the father but the variable mean is shifted by 1. Then, without initializing u it could be that you always accept the son move, so that your MC chain turns out to be a collection of multivariate random normal variables with mean 1. In this way you get an extra amount of 2 in your result. Note that this should also explain why the set of father to begin does not break the MC chain, since it is always thrown away from the statistics avoiding creating a bias.

Thank you very much for your response！ Actually I have figured my question out several hours after I asked this question. Here I'm glad to answer your doubts and sorry I haven't updated. — Mike, Feb 08 '18 at 14:43
and the 2nd: the segment: "scipy.stats.multivariate_normal(m, cov).rvs(1)", the meaning of the parameter 1 is not the mean of the distribution if i gave the m and cov, it 's meaning is the size of the sampling list which needed be generated. — Mike, Feb 08 '18 at 15:31
And 3rd: You can see that, in the if-else block, I append the result of a single sampling loop at the end of the list named "samples", whatever the result in that single sampling step is the son who was accepted or the father(which means the son was rejected), then i reset the variable "begin" as the last element of the list "samples", so when the next loop step comes, the value of the begin is passed to the "father" variable. So it's actually guarantee the chain goes right and meanwhile it's convenient to write the code, out of this reason, i implement the algo in that way. — Mike, Feb 08 '18 at 15:32

Get the expectation of random variables function's distribution by sampling from the joint distribution

Background of my question

Here my question comes

Update

1 Answers1