Finding Overlapping Line segments in 2D

Question

point a  = [1,0]   
point b  = [3,0]
point c  = [3,3]
point b' = [3,0]

Joining these points would give the line path a->b->c<-b' There is an overlap between b to c and back to b` to c. I want to find all the overlapping paths.

The problem I'm trying to solve is to identify these overlapping lines and draw them as curve lines so that user can distinguish them.

case 1

a = [1,0]
b = [5, 0]
c = [3, 0]

there is an overlap but user can clearly see the overlap, so i ignore this overlap.

case 2

a = [3,0]
b = [5, 0]
c = [1, 0]

Here if I draw straight line a-b path will be hidden. So in this case draw a curve line.

I have implemented the code by considering each N^2 combination of line and comparing their start and end lat long.

line AB = [ [1,0], [3,0]]
line BC = [ [3,0], [3,3]]
(AB == BC || AB == flip(BC))

Below are the code links

http://jsbin.com/qibarevodi/edit?js,console

http://bl.ocks.org/d/d21a0d3e6df2cd4bb08fbe2a6e66ceb8

Is there more efficient way to find the overlapping lines.

Answer 1

Here's what I would do. I will focus on a simplification of your problem, namely I will mark every line as "to be bent" if it overlaps with any other - Overlaps are bad. I'm not gonna make the distinctions that you did, as they are additional and not simplifying. Your questions then essentially assume the form:

Given a set of line segments in the plane, find the ones that overlap with others

If you still want to distinguish the cases you made, you will have to consider that they are ordered and do some extra checks. You could use an extra binary coordinate for their direction.

The first question is, how do we store the line segments? You seem to treat them specified as two points (x1,y1) and (x2,y2), which is why you do N^2 comparisons. I would suggest you threat them as lines with start and end point. That means, we are going to use as coordinates their slope m, y-axis intercept y, as well as x1, x2, Finding y and m should not be hard. Unfortunately this won't work for the y-axis itself. If you can't be sure that you have segments on the y-axis, you might need to modify this approach or think of some alternative for this specific case. Maybe give these a special key and keep the (y1,y2) values.

My suggestion now would be to store your lines in a hash table (maybe something like pythons dictionary) with key (m,y) and a list content [(x1,x2),(x1',x2'),...]. This allows you, for every segment, to only check the segments that lie on the same extended line. You can then go through all your lines once and mark the ones that overlap with another of the same key. Don't forget to use fast overlap test to do so.

If you want to pump up efficiency even further, you might want to take a look at Interval trees. I'm not too familiar with them myself, but theoretically you could use this data structure, or some modification thereof, for your intervals in the list for a given key to optimize finding overlapping ones. This is going to be important if you have many steps on one specific line. You could mark a line as bent as soon as it has an overlap with another in this tree.

Your algorithm might look something like:

• Project line segments onto slope and y-intersect (i.e. make the hash table)
• Loop through the hash keys
• For every element in the list, check if it overlaps with another one (this is where Interval trees might help you speed up further. It's also where your case distinction might come in)
• Mark the line as "to be bent" if the check is positive

Adressing some of the comments: Using only angle from x-axis won't help. Also, remembering the direction you came from won't help, as the following example should illuminate.

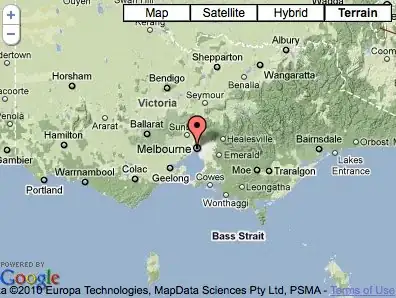
Note that, what exactly you test will depend on your desired outcome. You can test for overlap or maybe you can test if an interval is fully contained in another. It might also be worthwhile to read a bit into graph libraries and their visualizations, as your problem essentially describes a directed graph with fixed node positions. Hope some of this is of help to you.

Answer 2

Let's assume from your examples that you need to eliminate visual ambiguity for only a single polyline: one set of points connected by line segments. Handling more than one is not much more difficult, but I won't discuss it.

You really have two separate problems.

1. Identify sets of segments that lie on the same infinite line.
2. For each infinite line with segments, identify those that need to be represented as curves to disambiguate the traversal order of the points.

Part 1 is simple. Represent the infinite line that each segment lies on in a canonical form. Then build a map from canonical forms to lists (in polyline order for later) of the line segments that lie on them. A useful canonical form of an arbitrary infinite line is a unit direction vector d and the unique point p that lies closest to the origin. These are easy and fast to compute. For a segment between points a and b,

d = d' / length(d') where d' = [b.x - a.x, b.y - a.y]
p = d_perp (d_perp dot a) where d_perp = [d.y, -d.x]

Dealing with the case where points are very nearly on the same line, but not exactly, is a big additional topic. If you are interested in solutions, I can go into that further.

For part 2, we can consider each set of segments on the same infinite line L as a 1-d problem. It appears you're saying that when tracing the polyline, if any segment on L overwrites a vertex on L that has already been traced, the overwriting segment should be a curve. If this definition is accurate, it leads directly to simple algorithm:

for each line L
  let S be the subset of L already traced
  for each segment a->b lying in L (in polyline order taken from the map above)
    if a in S and b in S, then
      draw a->b with a curve
    else
      draw a->b with a straight segment
      add [a->b) to S

The notation add [a->b) to S means to add the line segment from a to b, but exclude the point b itself. This takes into account your case 1.

The pseudocode above is pretty abstract. How to represent the set S? Perhaps simplest is to rotate the points onto the x-axis. This is simple since you already have the canonical form for the line. Get the required x-coordinate for each point p with

x = d dot p

Now you can store S as the union of a set of 1d x-coordinate intervals. This can be done pretty easily with a balanced binary tree where where the keys are distinct intervals. (You don't need anything as sophisticated as an interval tree because you're storing a union, not overlapping intervals.)

Let me know if you have trouble working out the details. This is a nice little problem. For example, there are edge cases to think through. What if the same segment is repeated within the same polyline? You didn't give enough info about the problem to determine if this can happen.