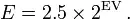I'd like to have a better understanding of the asymptotic notation and how can one classify whether a function is of O notation of another function, and how can we tell whether f = o(g) || f != o(g)
For example:
For example, how can we tell that f = O(g)?
I've seen mostly this approach (solution below is unrelated to the question above):
But this is confusing as I don't undertand the way the prove this.
Please help me understand the core concept that is being applied here.
Thanks
We say that f is O(g) if we can find these two things:
(1) We can find a constant "C" (You pick only one constnat , here i mean you can't change it later, this is most confusing part for beginners).
(2) And a "N" (This is some lower bound, means for values greater than this N, our formula will be valid, once you reach end then come back and try to understand i mean by lower bound).
such that whenever we plug in the value of n>= N then f(n) should be less or equal to C.g(n)
Or in formula form:
Example:
let's say i have a function f = 3n^2 + 4n + 3
and one more function g = n^2
Is f = O(g)?
The leading term of f is 3n^2 , it means if i have a constant higher than 3 and i multiply it with g then f will be less than g.
Let's take n = 4 > 3 then i get g = 4n^2 and my constant c is then 4.
Now the question is what happends if i increase the value of n? If i plug in for example n = 4 then f(n) will not be less than g(n) but when i insert n = 5 then it is valid. so in this example c = 4 and N = 5.
Now you have two different things in your question. This question below has nothing to do with Big-O notation , it's called tilde notation.
Big-O throws constant terms away but tilde does not. It's more stricter form for the comparisons of algorithms. Here 22 means whenever n approaches infinity, the difference between f and g is approximately 22. However i prefer tilde notation but first you need to understand Big-O then you can go further.
For your this question :
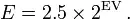
You can see: both function have higher terms n namely f = 7n + ... and g = n.
If i want to prove is f is o(g)
Now if i ask for what value c c.g(n) is greater than f(n).
Does there exist any constant c such that the formula is valid for all n >= some N.
If i multiply g now with 7 (because f has leading constant 7) would this be valid? No because f has also factor of 8 with it, it means i need to increase constant c. Let's take it as 8 then still 7n + 8 > 8n if n = 1 but what happends when n >= 2 then g is always greater than f. So for constant c = 8 and n >= 2 f is o(g). You can also prove also that g is O(f).
This is not difficult, you should get constant c = 1 and for n belonging to natural number
A function f on natural numbers is Big-Oh of a function g on natural numbers, written f(n) = O(g(n)), if and only if there exist constants c > 0, n_0 > 0 such that, for n >= n_0, f(n) <= c * g(n). To prove this, you must show values for c and n_0 that work and show that they work. You can show that 7*n + 8 = O(n) because 7*n + 8 <= 8n for all n >= 8 (c = 8, n_0 = 8). You can show that n = O(7*n + 8) because n <= 1 * (7*n + 8) for n >= 1 (c = 1, n_0 = 1).
A function f on natural numbers is Little-Oh of a function g on natural numbers, written f(n) = o(g(n)), if and only if for all constants c > 0, there exists an n_0 such that f(n) < cg(n) for n >= n_0. To prove this, you must show how to find a n_0 that works given any positive value of c. You can show that 7*n + 8 = o(n^2) because 7*n + 8 < c*n^2 can be rearranged to c*n^2 - 7*n - 8 > 0, which clearly has solutions for any positive choice of c (the derivative is 2*c*n - 7 which is eventually always positive, so the function must get positive for a large enough n_0).
