0

To construct a contractive autoencoder, one uses an ordinary autoencoder with the cost function enter image description here

To implement this with the MNIST dataset, I defined the cost function using using tensorflow as 

def cost(X, X_prime):
    grad = tf.gradients(ys=X_prime, xs=X)
    cost = tf.reduce_mean(tf.square(X_prime - X)) + tf.reduce_mean(tf.square(grad))
    return cost

and used AdamOptimizer for backpropagation. However, the cost doesn't go any lesser than 0.067, which is peculiar. Is my implementation of the cost function incorrect?

Edit: After reading the documentation ontf.gradients, the above implementation would have computed 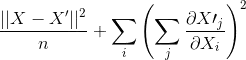enter image description here instead. So my question is, how do you do derivatives component wise in tensorflow?

Chester Cheng
  • 158
  • 1
  • 10

2 Answers2

1

To address your post-edit question: TensorFlow doesn't have a function that computes Jacobians. The following quote, taken from a Github discussion, sketches how you might compute the Jacobian yourself:

Currently, you can compute the Jacobian of, say, a vector, by calling gradients multiple times, one for every scalar component (obtained by slicing) of the original vector, and reassembling the results.

Akshay Agrawal
  • 912
  • 5
  • 7
0

So just like Akshay suggested, the way to compute the Jacobian is through slicing the differentiation target. Below is a little example.

enter image description here

The Jacobian matrix of f is

enter image description here

The code in tensorflow

X = tf.Variable(tf.random_normal(shape=(10, 3)), dtype=tf.float32)
y = X[:, :-1]

jacobian = tf.stack([tf.gradients(y[:, i], X) for i in range(2)], axis=2)

sess = tf.Session()
j = sess.run(jacobian)
print(j[:, 0, :])

array([[1., 0., 0.],
       [0., 1., 0.]], dtype=float32)

Which gives

Chester Cheng
  • 158
  • 1
  • 10