Python: define color curve section

Question

I am trying to replicate the following figure:

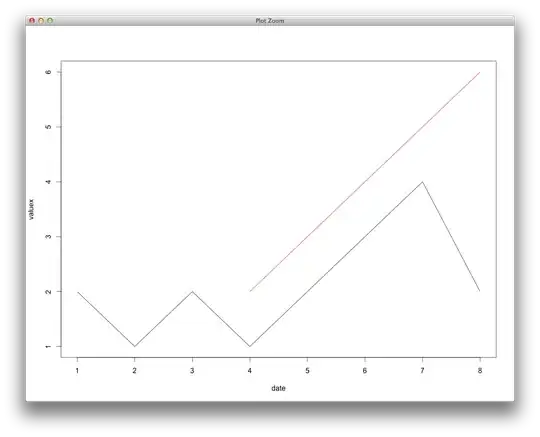
The color gradient goes from blue to red and indicates the state of a material. I can currently plot each curve. Each line is defined by two points, and is then simply plotted using pyplot (matplotlib library). I also have a clear idea on how to compute the associated value.
However, it can be noticed, for example for point 9 or 22 on the first figure, that the value is different at the overlapping area. I have currently no clue on how to do that effectively.
The only idea I have comes from this solution. Basically, I have to turn each curve section into a polygon. But it looks very heavy, and prehaps not the best solution in this case.

I am mainly asking for leads that could help me to achieve this, or just a smarter way to look at the problem !

The code that produced this figure:

import shelve
import matplotlib.pyplot as plt
import os

path = "C:/Users/***/Desktop/Python/PyHugo/"
d = shelve.open(os.path.join(path, 'output.db'))
pointMat = d ['curve']
d.close()

fig=plt.figure()
ax=fig.add_subplot(111)

for matID in pointMat.keys():   
    for couple in range(len(pointMat[matID])-1):
        plt.plot([pointMat[matID][couple][0][0],pointMat[matID][couple][1][0]],[pointMat[matID][couple][0][1],pointMat[matID][couple][1][1]])

plt.show()

Points are stored in the pointMat dictionnary. Each area has a set of points. An area is a specific material. It is represented on figure one by le black line (around 540). So in the current example there are 2 materials.

The, the first set of points is given by:

print matPoint[0][0]

results : [[20, 20], [0, 40]]. We asked for the first couple of point in the first material.

Edit 1: code added, off-topic question removed

EDIT 2: Instead of plotting the curves, I am mapping the values over a grid (discretisation of the phenomena). The problem has too many variations, and this seemed a better idea. Thank you for the time spend trying to help me !

score 0 · Answer 1 · answered Nov 13 '17 at 14:58

0

You need to make your lines semi-transparent using the alpha parameter:

plt.plot([pointMat[matID][couple][0][0],
         [pointMat[matID][couple][1][0]],
         [pointMat[matID][couple][0][1],
         [pointMat[matID][couple][1][1]],
         alpha=0.7)

as an example.

answered Nov 13 '17 at 14:58

Colin Dickie

910
4
9

Thank you for your answer. However, the colors on Figure 1 are not pure style, and depict the physic behind the phenomena. For example on point 9, you can see that the curve on the left of the interface has the same color as the intersection between both curve on the right. On the intersection just below, curve 3 has the same value as the intersection of curves 1 and 4. This is the tricky part. – MaximeS Nov 13 '17 at 15:47
@MaximeS i don't know the physics underlying this. But from points 22 and 36 they both appear to get darker as the two lines overlap. This is exactly what I'd expect from overlaping two colours of <1 opacity/alpha. In general the lighter colours are more transparent (low alpha) and as they get overlain with more lines they get darker (less transparent). Would this follow from the physics? – Colin Dickie Nov 13 '17 at 16:25
To be honnest with you I thought the idea of transparency was good, but sadly the maths did not follow along, or at least only very partially (congrats, it worked on point 22 !! ). For example, that would not work at all for the inetersection at [240,360]. However adding the values of the intersecting curve could create something good ! I'll look into it – MaximeS Nov 13 '17 at 16:47

Python: define color curve section

1 Answers1