0

I was going through a licensed guide to represent product families as a bag model in which occurrences are also taken into consideration to come up with a BDD.

I am trying to include the similar steps into my problem. The text says

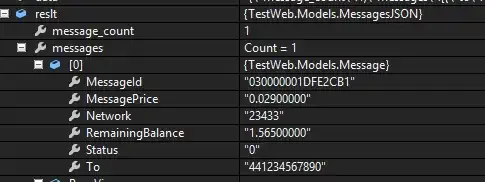
If we adopt the bag-model, the implementation is similar to the set-model implementation except for handling the duplications of features. ROBDDs do not allow duplications of nodes. To handle the number of occurrences of a feature within the BDD itself, we have devised occurrence levels that encode it. We encode this number binary. For example, if we have a product with 3 features: x, y and z, and the maximum number of occurrences of a feature is seven, then we need three binary bits to encode it. Let the product family W have one product with three x features and six z features and zero y features. Our product family contains a product Pt, represented by the BDD in Figure 3.7. The BDD representing this bag describes the product in a way similar to that in the set model. However, we encode the occurrences in the levels of nodes containing bl, b2 and b3. We read in Figure 3.7 that, if x exists in this product, then we have to select bl and b2, but not b3. This is the binary code 011 representing b3, b2 and bl respectively which carries the occurrence of three for x. Similarly, for y to exist in this product, we get the binary occurrence encoding to be 000 which is 0 occurrences. For z, we get the binary occurrence of 110 which carries the number six.

So by this, for a product family Z = {{(x,3),(y,0),(z,6)}} the corresponding bdd would be ->

BDD

for a product Family W = {{(x,3),(y,1),(z,7)}} the BDD would be

BDD2

But how did he come up with these BDDs, there must be some underlying formula for the BDDs. Could you please help me understand how to arrive at the same formula for a given family so that i can further use it similarly in my other use cases. Thanks.

0 _
  • 10,524
  • 11
  • 77
  • 109
Vishal Tyagi
  • 560
  • 9
  • 26
  • What is a "product family"? – 0 _ Nov 12 '17 at 20:01
  • Thanks for your interest, product family here can be considered as a set of features that a product has. In bag model we also take into consideration the occurrence with the feature in the product. – Vishal Tyagi Nov 13 '17 at 09:38
  • If its of any help, there is this link that states similar concept https://pdfs.semanticscholar.org/2f6b/c6a5b5d78906e4ff98d3ea883963dbb1ed6a.pdf – Vishal Tyagi Nov 13 '17 at 09:39

1 Answers1

0

A bag is a collection of elements with multiple occurrences. The standard module Bags in the Temporal Logic of Actions (TLA+) contains a mathematical definition that corresponds to bags.

To convert from the graph of a binary decision diagram to a formula, I used the code below. The answer for the first BDD from the OP is:

 /\ b \in 0 .. 7
 /\ x \in 0 .. 1
 /\ y \in 0 .. 1
 /\ z \in 0 .. 1
 /\  \/ (b = 0) /\ (y = 1)
     \/ (b = 3) /\ (x = 1)
     \/ (b = 6) /\ (z = 1)

This expression is written in TLA+.

The above actually is not a bag, because a bag contains at least one occurrence of each element (so no occurrences of y means that this isn't a bag; omitting y should turn it into a BDD corresponding to a bag). Whether a bag is a suitable representation for product families is a separate concern, which I will not discuss.

You can adapt the code to confirm the formula for the BDD shown in the second figure.

The below code uses the Python packages omega == 0.1.1 and dd == 0.5.1 (note: I'm an author of them). These work in pure Python, which suffices for BDDs of this size (otherwise building dd.cudd will let you use CUDD--of course that makes no difference for BDDs that are small enough to write by hand).

#!/usr/bin/env python
"""Convert from a BDD figure to a formula."""
from omega.symbolic import fol

# "bare" BDDs (without integers) can be used also
# via the package `dd`
# from dd import autoref as _bdd

# bdd = _bdd.BDD()

ctx = fol.Context()
ctx.declare(x=(0, 1), y=(0, 1), z=(0, 1), b=(0, 7))

bdd = ctx.bdd
# bdd.declare('x', 'y', 'z', 'b1', 'b2', 'b3')

# level of b3
u1 = bdd.add_expr('b_2')
u2 = bdd.add_expr('~ b_2')
# level of b2
u3 = bdd.add_expr(f'ite(b_1, {u1}, FALSE)')
u4 = bdd.add_expr(f'ite(b_1, FALSE, {u2})')
u5 = bdd.add_expr(f'ite(b_1, {u1}, {u2})')
u6 = bdd.add_expr(f'ite(b_1, {u2}, FALSE)')
# level of b1
u7 = bdd.add_expr(f'ite(b_0, FALSE, {u3})')
u8 = bdd.add_expr(f'ite(b_0, FALSE, {u4})')
u9 = bdd.add_expr(f'ite(b_0, FALSE, {u5})')
u10 = bdd.add_expr(f'ite(b_0, {u6}, {u3})')
u11 = bdd.add_expr(f'ite(b_0, {u6}, FALSE)')
u12 = bdd.add_expr(f'ite(b_0, {u6}, {u4})')
u13 = bdd.add_expr(f'ite(b_0, {u6}, {u5})')
# level of z
u14 = bdd.add_expr(f'ite(z_0, {u7}, FALSE)')
u15 = bdd.add_expr(f'ite(z_0, {u9}, {u8})')
u16 = bdd.add_expr(f'ite(z_0, {u10}, {u11})')
u17 = bdd.add_expr(f'ite(z_0, {u13}, {u12})')
# level of y
u18 = bdd.add_expr(f'ite(y_0, {u15}, {u14})')
u19 = bdd.add_expr(f'ite(y_0, {u17}, {u16})')
# level of x
from_fig = bdd.add_expr(f'ite(x_0, {u19}, {u18})')

# the variable order from the first figure in the OP
levels = dict(x_0=0, y_0=1, z_0=2, b_0=3, b_1=4, b_2=5)
fol._bdd.reorder(bdd, levels)
bdd.dump('foo_1.png', [from_fig])
# a better variable order
levels = dict(b_0=0, b_1=1, b_2=2, x_0=3, y_0=4, z_0=5)
fol._bdd.reorder(bdd, levels)
bdd.dump('foo_2.png', [from_fig])

# Create the BDD directly from an expression
s = r'''
    \/ (b = 3 /\ x = 1)
    \/ (b = 0 /\ y = 1)
    \/ (b = 6 /\ z = 1)
    '''
from_formula = ctx.add_expr(s)
assert from_formula == from_fig

# print a minimal formula in disjunctive normal form
# use this to covert BDDs to expressions
print(ctx.to_expr(from_fig, show_dom=True))

The dependencies can be installed with pip:

pip install dd==0.5.6
pip install omega==0.3.1

enter image description here

By reordering the levels of variables as done in the above code, we can obtain a smaller (RO)BDD:

enter image description here

The above BDDs are represented using negated edges, which are explained in this tutorial on BDDs.

0 _
  • 10,524
  • 11
  • 77
  • 109