Which algorithm can efficiently find a set of points within a certain distance of a path?

Question

Given a set of points s (a set of x,y coordinates) and a path that is made up of line segments joining a set of points l, describe an efficient algorithm that can be used to find a subset of points from s that are within the specified distance d of the path l.

A practical application of this may be to find a list of restaurants within 10 miles anywhere along a road trip path between cites.

For example, in the following diagram, the points in green would be included in the search results.
_{(source: flickr.com)}

Solutions would be preferred in C#, but bonus points may be given for a SQL based approach :-)

Answer 1

I also thought about this some time ago. I think, efficient is misleading. Just testing all line segments for each point is good enough. It is very cheap to calculate the distance. If there are many points, you can also think about refining the strategy which points to choose using a level-set approach. i.e.

• go along the line, step width 2x the distance you want to check (more or less?) and create artificial points that are "near".
• itereate: pick new points around points that are "near" (don't calculate an eucledian distance, just a 1-norm and simply test the x and y coordinates) - then test their distance (you can even inherit the specific line segment from the artifical points to the found "near" points and select that one first for testing, but broaden the search, since there could be twists!)

that's maybe not complete, but should be fast and avoids checking points far away and quite ok.

Answer 2

1. Define a "left road" and "right road": for each line segment of the original path, create a line segment d units to the "left" and one d units to the "right" of the segment.

2. Connect the left road and right road at the ends to make a polygon.

3. Apply a standard algorithm to determine which points of interest lie inside the polygon.

Answer 3

1.) Store your points in a SQL Server 2008 table using the geometry datatype (or geography, if they're defined using coordinates of lat/long) Here's a script to create 100 sample points distributed randomly between (0,0) and (40,20):

DECLARE @Points table (
  id int,
  position geometry
  );

DECLARE @i int = 0, @x int, @y int;
WHILE (@i < 100)
BEGIN
  INSERT INTO @Points VALUES 
    (@i, geometry::Point(RAND() * 40, RAND() * 20, 0))
  SET @i = @i + 1;
END

2.) Define your line as a linestring, using the same datatype and SRID as for your points:

DECLARE @line geometry = 'LINESTRING(0 10, 10 15, 20 8, 40 10)';

3.) Use the STDistance() method in a predicate of a SELECT query against the points table. For example, to select all points within 5 units of the line:

SELECT * FROM @Points
WHERE @line.STDistance(position) < 5;

What's more, since the spatial methods of SQL Server are available in a redistributable dll (Microsoft.SqlServer.Types.dll - part of the SQL Server feature pack http://www.microsoft.com/downloads/en/details.aspx?FamilyID=ceb4346f-657f-4d28-83f5-aae0c5c83d52), you can use this same approach in either C# or direct in SQL Server.

Answer 4

Tough homework assignment eh?

Perhaps a good start might be to look at breadth-first pathfinding algorithms- maybe something like a flood-fill approach would be useful for this?

Edit: So if it just looks like a homework assignment, maybe I can be more helpful...

I would first look to define a rectangle containing the line and the points that could be within it as that may enable us to get rid of a large number of points that are nowhere near our line.

For each point you could then create a square, representing the list of points within the radius of that point. This is again a way of reducing the number of elements to search.

Unfortunately I don't know enough geometry to be aware of a clever way of deciding whether a list of points fall inside or outside of a circle aside from simply calculating the distance between them and the centre of the circle through basic trig- I'm sure there is one. By using the aforementioned simple subdivision or some variant on it you should find that you can pre-emptively reduce the number of possible points that need to be searched through.

Also if you keep all your points to search in one list and remove the ones that are hits for the first circle, when it comes to measure subsequent shapes. I've used a brute-force version of this to do simple postcode-distance checks based on location data - that is documented in quite a few places online, but running it down a path would probably be quite computationally expensive.

This geometric approach would probably be better for a situation where you weren't doing a lot of repeated searches- if there are many in a row you might want to organise your ponts into a network so that you can use standard pathfinding on them. It would be worth doing some protoyping to see which is more efficient, but I would expect that if you were to create an appropriate network to represent your data you could then be more flexible in how you search it.

Answer 5

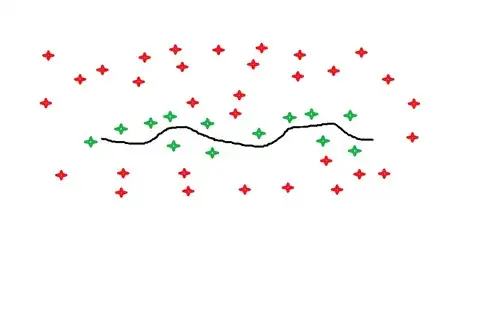
The only solution to this is along the lines of:

for each point
  for each line
    is distance to line within constraints

The inner loop can be terminated early once a point that lies within the constraint is found. Note that the inner and outer loops can be transposed.

The question then becomes one of determining if a point is within the constraint. mbeckish suggests using a simple rectangle test, where the rectangle is formed by extruding along the line's perpendicular, but this will fail for points near the end points but outside this rectangle. Extruding the rectangle along the direction of the line as well will also fail since the points near the end should really use a point in circle test:

|-------------
| *    /
|    --
|   /
|  /
| |
| |
|/
|         |--------| <- the line segment

where the * is inside the expanded rectangle but outside the rounded end cap which would be a more strict test.

Now, the distance test might not be a 'as the crow flies' test but a graph search, for example, points within x miles of a road using only roads to connect them together:

--------------------------------------------------- < the road
   |
   |              * <- target
...|..............|................................ < check distance
   |              |
   |--------------| <- roads to target

In the above diagram, the target is within the search area but to get to the target along the available roads would be greater than the allowed distance.

However you choose to implement the test, the basic loop in a loop algorithm will be required.

Ways to check the constraint where the constraint is an 'as the crow flies' constraint:

1. Geometrically: First, determine the distance from the point P to the line. Then, if the point is within the constraint project the point P onto the line segment, where the line is defined as:

   L = P1 + (P2-P1).n
   

   where P1 and P2 are the end points and n is the parametric variable. If the value of n for the projected P is in the range 0 <= n <= 1 then the point is between P1 and P2. Finally, do a point in circle test for circles centred on P1 and P2.

2. Transformations: Create a transformation matrix for each line segment such that P1 is transformed to the origin and P2 is transformed to (|P1-P2|, 0). Then apply each transform to all points and then test each point in the rectangle (0, -constraint) - (|P1-P2|, constraint). This method can be highly optimised using SIMD or a GPU

3. Graphically: Draw the line segments to a bitmap using a pen with rounded end caps and a width proportional to the constraint distance. Then, for each test point, check the pixel in the bitmap corresponding to the point. This is not accurate (but bigger bitmaps create more accurate results but need more memory) but is pretty quick once the bitmap is created.

   If the constraint is defined by the route along a graph it becomes more complex. You need to look at breadth first searches where the start points are the end of each line segment and the end point is the potential target. If a line segment has junctions along its length, then break the line segment into segments without junctions.

Answer 6

I'm not really sure if I understand the question correctly, but wouldn't Dijkstra's algorithm fit? It finds the shortest paths from a source node, and you can just abort after you reached you maximum distance and check which points from s have already been found. I'm not sure how well it plays with SQL though.

Answer 7

If you want to do at least some of the work in SQL, you can compute a bounding box for the path, then incorporate into your query the condition that the location is inside the bounding box. You run one of the other algorithms against just the returned rows.

This at least prevents you from having to download the entire data base for each path.

Answer 8

I'm surprised no one has mentioned the A* alogirithm for this. It seems like a perfect fit. What am I missing here? If you're not familar with it, google and ye shall find =). (Yes, it does come from the gaming world...)

Answer 9

Could you use a quad-tree to partition the space up into segments, and then only for points in the segments close to your path?

Answer 10

You should be able to accomplish this through vector math and trig though the exact methods escape me.

For each line segment calculate the values need to transform a point from world coordinates to local coordinates relative to the line segment (so any point run through the calculation would be relative to a coordinate system where the line segment is the x-axis)

For each point run the following checks:

1- If the point is within distance of either end point we know that it should be included. This is accomplished by a simple distance^2 <= (x2 - x1)^2 + (y2 - y1)^2 calculation between each endpoint and the target point.

2- Run the target point through the transformation. After the transformation if x >= 0 and x <= (length of the line segment) and |y| <= distance then the target point should be included otherwise it should be excluded.

My vector math is a bit rusty so I can't provide better code/examples sorry! But maybe my post will inspire someone else to write out the proper way to do it.

Answer 11

I believe these two classes will answer your question. I built the GetArea() function using Heron's Formula. Make sure that the Segment Points are always passed first to the IsPointWithinDistanceToLineSegment and the TestPoint is always passed 3rd.

EDIT: I stupidly used Point which only allows integers for X and Y. You'll need to fix this with another class that takes doubles or floats as X and Y...

public class Geometry
{
    public static double GetDistanceBetweenTwoPoints(Point SegmentStart, Point SegmentEnd)
    {
        return Math.Sqrt(Math.Pow(SegmentEnd.X - SegmentStart.X, 2) + Math.Pow(SegmentEnd.Y - SegmentStart.Y, 2));
    }

    public static bool IsPointWithinDistanceToLineSegment(Point SegmentStart, Point SegmentEnd, Point TestPoint, double TestDistance)
    {
        if (GetDistanceBetweenTwoPoints(SegmentStart,SegmentEnd) <= TestDistance || GetDistanceBetweenTwoPoints(SegmentEnd,TestPoint) <= TestDistance)
        {
            return true;
        }
        var T = new Triangle(SegmentStart, SegmentEnd, TestPoint);
        var BaseLength = GetDistanceBetweenTwoPoints(SegmentStart, SegmentEnd);
        var Area = T.GetArea();
        var TriangleHeight = 2* Area / BaseLength;
        return T.AB >= T.BC && T.AB >= T.AC && TriangleHeight <= TestDistance;
    }
}

public class Triangle
{
    public Triangle(Point a, Point b, Point c)
    {
        this.a = a;
        this.b = b;
        this.c = c;
    }

    public Point a
    {
        get;
        set;
    }

    public Point b
    {
        get;
        set;
    }

    public Point c
    {
        get;
        set;
    }

    //Lengths of Sides
    public double AB
    {
        get
        {
            return Geometry.GetDistanceBetweenTwoPoints(a, b);
        }
    }

    public double AC
    {
        get
        {
            return Geometry.GetDistanceBetweenTwoPoints(a, c);
        }
    }

    public double BC
    {
        get
        {
            return Geometry.GetDistanceBetweenTwoPoints(b, c);
        }
    }

    public double GetArea()
    {
        var Term1 = Math.Pow((Math.Pow(AB, 2) + Math.Pow(AC, 2) + Math.Pow(BC, 2)), 2);
        var Term2 = 2 * (Math.Pow(AB, 4) + Math.Pow(AC, 4) + Math.Pow(BC, 4));
        var result = .25 * Math.Sqrt(Term1 - Term2);
        return result;
    }
}

Answer 12

Given general computing tools, your best algorithm is going to be some variation on filtering out obviously uninteresting points and finding the distance from every line segment to each remaining point. (The polygon solution suggested is wrong -- the area of interest is the union of that polygon with the circle of radius d around each point on l -- and actually less efficient than simply finding the distance from each point to every line segment.)

Which filters are best will depend on the nature of your data -- for instance, in the sample diagram, filtering on l's bounding box (plus d) will be very useful.

An interesting filter would be: given point p defining l, take a circle of radius r, where r is the maximum length of the two segments defined in part by p plus d. Only points within this circle can be close enough to those two segments to be in our solution set, so we can quickly determine whether or not we can skip those two line segment distance calculations. (This will be less efficient if some line segments are very long, but if they are, those line segments can be easily broken up into smaller chunks.)