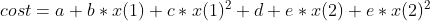0

I am trying to convert my quadprog linear quadratic problem over to fmincon so that later I can add nonlinear constraints. I am having difficulty when I compare my solutions using the two methods (for the same problem). The odd thing is that I get very different cost output when I get almost the same x values. Below is a simplified case of my code without constraints.

Here, my objective function is

cost = a + b*x(1) + c*x(1)^{2} + d + e*x(2) + f*x(2)^{2}

%objective function
% cost = a + b*x(1) + c*x(1)^2 + d + e*x(2) + e*x(2)^2 
param = [1;2;3;4;5;6];
H = [2*param(3) 0; 0 2*param(6)];
f = [param(2); param(5)];
x0 = [0,0];

[x1,fval1] = quadprog(H,f);
[x2,fval2] = fmincon(@(x) funclinear(x,param), x0);
fval1
fval2


%% defining cost objective function
function cost = funclinear(x, param);
    cost=(param(1) + param(2)*x(1) + param(3)*(x(1))^2+ param(4) +param(5)*x(2)+param(6)*(x(2))^2);
end

My resulting x1 and x2 are 

x1 =[-3.333333333305555e-01;-4.166666666649305e-01];
x2 =[-3.333333299126037e-01;-4.166666593362859e-01];

which makes sense that they are slightly different since they are different solvers.

However my optimized costs are

fval1 =-1.375000000000000e+00;
fval2 =3.625000000000001e+00;

Does this mean that my objective function is different than my H and f? Any help would be appreciated.

user3546200
  • 269
  • 1
  • 3
  • 10

1 Answers1

1

In the quadprog formulation, the constant terms a and d are not considered.

param(1)+param(4) = 1 + 4 = 5

The difference of your results is also 5.

Daniel1000
  • 779
  • 4
  • 11
  • Does this mean that fmincon's x values are more precise because it incorporates constant terms? (and its fval would be the correct one?) – user3546200 Oct 03 '17 at 15:16
  • If you add a constant value to an objective function, the minimum stays exactly the same! The quadprog solver yields the most precise results numerically, because quadratic of problems can be solved exactly with a finite number of steps. fmincon works iteratively, until some stopping criterion is reached (StepTolerance, OptimalityTolerance etc.). If you need not only the x values but also also the final objective function value, you have to add a+d manually in the quadprog case, of course, to match your original problem. – Daniel1000 Oct 03 '17 at 15:22
  • Careful. Convex (!) quadratic problems might be solved in polynimial-time exactly using rational-arirthmetic, but no practical solver is doing that. Bit-complexity and algebraic complexity differs. This results pretty much in: all interior-point based solvers (for convex problems) are polynomially bound when targeting some a-priori know duality measure. But this is probably the same for fmincon,but hard to check as there are many different algorithms within fmincon, including an interior-point solver.But most of these achieve the same kind of convergence in theory although practice can be diff – sascha Oct 04 '17 at 06:36
  • To sum up: these methods are all iterative, all proven to be converging in polynomial-time (in convex case) to some approximation and all are using similar convergence-criterions. But quadprog should behave better in practice as it's more constrained, more tuned for the non-general convex-optimization of CQP. (commercial solvers will make the final result exact using Simplex, often on-top of the IPM-solution in the LP-case, i'm unsure about the CQP-case ). – sascha Oct 04 '17 at 06:45