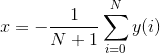6

How would I solve an equation containing a summation expression, i.e. something like.

Simple Equation

I would consider the following code fragment to solve this equation: 

from sympy import *

i, N, x = symbols("n, N, x")
y       = Function("y")
eq      = summation(x + y(i), (i, 0, N)) 

print solve(eq, [x])

However, while this equation is simple solve() does not produce a result. The expected solution would be

enter image description here

Frank-Rene Schäfer
  • 3,182
  • 27
  • 51

1 Answers1

3

I believe the plain answer is that it's just too complicated for the currecnt system to make the substitutions required.

With that said, there might be an issue with expansion of summation here.

I managed to get the correct answer by changing the Sums in the expand output with summations, see console session below.

The reason which I believe made the last one possible, is that summation(x, (i, 0, N)) evaluates to x*(N + 1) (effect of the summation function), while the Sum(x, (i, 0, N)) returned by the expansion remains a simple Sum object, therefore no substitution made for it after the inner expansion in the solve function.

>>> from sympy import *
>>>
>>> i, N, x, y = symbols("i, N, x, y")
>>> eq         = summation(x + y(i), (i, 0, N))
>>>
>>> expand(eq)
Sum(x, (i, 0, N)) + Sum(y(i), (i, 0, N))
>>>
>>> solve(summation(x, (i, 0, N)) + summation(y(i), (i, 0, N)), x)
[Sum(-y(i), (i, 0, N))/(N + 1)]
  • By the way, the solution is divided by N + 1, since the summation contains 0 and N (thus, 0 to N is N + 1 times).
Uriel
  • 15,579
  • 6
  • 25
  • 46
  • 1
    I think, you hit the point. The `solve()` function does not seem to make the `expand()` step at the current state of development. And, you are right, of course, with the `N+1`. – Frank-Rene Schäfer Oct 02 '17 at 08:44
  • @Frank-ReneSchäfer I added a last paragraph, `The reason which...`. I believe that's why, and if so it is probably an unintended bug. – Uriel Oct 02 '17 at 08:46