1

I am trying to get the frequency response of any transfer functions using the Fourier transform of the impulse response of the system. It works pretty well for most of the cases tested but I still have a problem with transfer functions in which there is an integrator (e.g. 1/s ; (4s+2)/(3s^2+s) etc.).

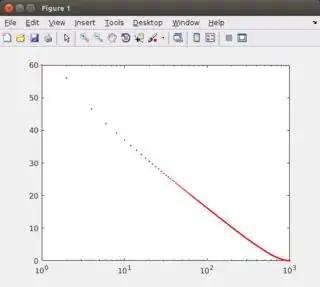
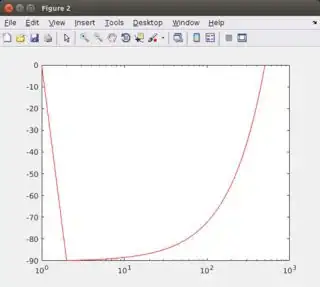
Let's take the example of a pure integrator with H(s) = 1/s. The impulse response obtained is a step function as expected but then, the Fourier transform of the impulse response does not give the expected theoretical results. Instead it gives really small results and do not lead to the classic characteristics of an integrator (-20dB/decade magnitude and -90deg phase) after processing.

Maybe a few lines of codes can be helpful if I was not clear enough:

h = tf(1,[1 0]);
t_step = .1;
t = [0 : t_step : 100000]';
[y,t1] = impulse(h,t);
y_fft = fft(y);

Do you know where this problem may come from? If you need further information, please let me know. I am working on MATLAB R2013b.

Filburt
  • 17,626
  • 12
  • 64
  • 115
J-D
  • 13
  • 2
  • The problem is related to: (1) `fft` assumes a periodic signal, i.e. an infinite repetition of the provided discrete signal, and (2) you should also include the response for negative times, i.e. before the pulse occured. – m7913d Sep 01 '17 at 11:00
  • @m7913d Concerning the first point you made, I do not understand how this problem could not occur for any other transfer function but for the integrator. Can you please explain? Also, I have already tried to add the negative times and I could not see much change. – J-D Sep 01 '17 at 11:40

1 Answers1

0

As mentioned in my comment, the problem is related to:

  1. fft assumes a periodic signal, i.e. an infinite repetition of the provided discrete signal
  2. you should also include the response for negative times, i.e. before the pulse occured.
h = tf(1,[1 0]);
t_step = 1;
t = [0 : t_step : 999]';
[y,t1] = impulse(h,t);

y = [y; zeros(1000, 1)];
y_fft = fft(y);

figure
semilogx(db(y_fft(1:end/2)), 'r.');

figure
semilogx(180/pi*angle(y_fft(y_fft(1:end/2)~=0)), 'r');

enter image description here enter image description here

Further remarks

  • Note that due to the periodicity of the fft (and y), half of the values are minus infinity, which I did not plot to obtain a nicer result.

  • Note that the effect of the difference between the fft and the continuous fourier transform depends on the real fourier transform of the impulse response. Especially aliasing may be a problem.

m7913d
  • 10,244
  • 7
  • 28
  • 56
  • It works indeed, sorry I must have mistaken. However, I cannot manage to have the argument constant and equal to 90 degrees, even with this method. Can you? – J-D Sep 01 '17 at 13:02
  • @J-D I tried to explain it somewhat further, but maybe there are also some other effects I forgot to mention. – m7913d Sep 01 '17 at 19:00