I have a graph and I calculated the degree distribution and degree as follows:
library(igraph) # for these two functions
dd <- degree_distribution(graph)
d <- degree(graph)
From this, I estimated to Power Law, to see if my distribution follows the "Law of Power":
degree = 1:max(d)
probability = dd[-1]
nonzero.position = which(probability != 0)
probability = probability[nonzero.position]
degree = degree[nonzero.position]
reg = lm(log(probability) ~ log(degree))
cozf = coef(reg)
power.law.fit = function(x) exp(cozf[[1]] + cozf[[2]] * log(x))
From that, I plotted the points and power law using ggplot2.
Resulting in the following image:
df <- data.frame(x = degree, y = probability)
print(
ggplot(df, aes(x,y,colour="Distribuição"))+
geom_point(shape = 4) +
stat_function(fun = power.law.fit, geom = "line", aes(colour="Power Law"))+
labs(title = "Grafo", subtitle = "Distribuição dos Graus",
x="K", y="P(k)", colour="Legenda")+
scale_color_brewer(palette="Dark2")
)
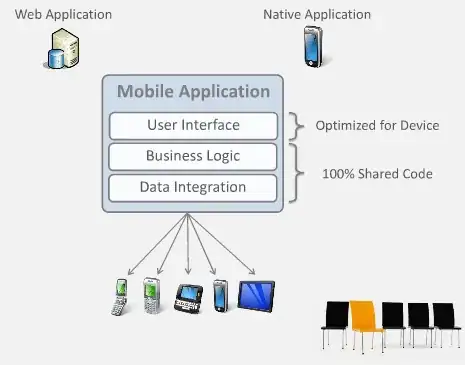
As you can see, my distribution does not follow Power Law! I would like to estimate the Poisson distribution and plot on the same graph. Even though I'm not sure that my distribution does not follow (or follow) Poisson, I would like to draw it together with Power Law. I have no idea how to estimate this distribution (Poisson) from the data, and calculate the average degree.
Can anyone help me?
The graph used to calculate the distribution and the degree is very large (700 thousand vertices), so I did not put the data of the graphs. The explanation of the answer can be based on any graph.