3

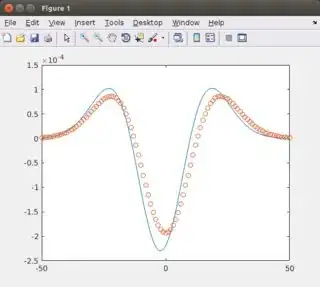
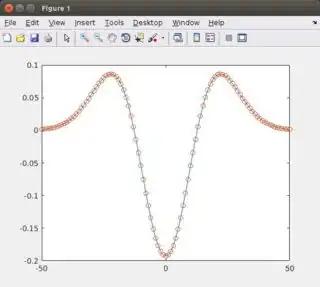
I am writing MATLAB code with the intention to do some fittings. I simulated a plot using a second-order Gaussian (see my code below) and tried fitting using the lsqcurvefit function. Unfortunately, MATLAB returns the same guess values as 'optimized' parameters and apparently gets stuck in a local minimum.

Can someone please provide some advice as to what might be wrong here? I know that if the guess is far from the 'true' values then this can happen, but I expected MATLAB to return an answer which was closer to true value. Improving the initial guess to [29,0] (which is much closer to the actual value) results in the same output: that the initial value is a local minimum.

%%%%%%%%%%

function z= testfunction(x, xdata);

sigma=x(1)/(2*sqrt(2*log(2)));

z=((xdata.^2-2*x(2)*xdata-sigma.^2+x(2)^2)./(sigma^5*sqrt(2*pi))).*exp(-(xdata-x(2)).^2/(2.*sigma.^2));

end
%%%%%%%%


% Simulate Data

xdata= -50:1:50;

ydata = testfunction([30,0],xdata);

% Fit Data 

xfit = lsqcurvefit(@testfunction,[19,-4],xdata, ydata );

xfit(1)
xfit(2)

yfit=testfunction([xfit(1),xfit(2)],xdata);

% Plot Data;
plot(xdata,yfit);
hold on;
plot(xdata,ydata,'o')

Output: 

Initial point is a local minimum.

Optimization completed because the size of the gradient at the initial point 
is less than the default value of the optimality tolerance.

<stopping criteria details>


ans =

    19


ans =

    -4
m7913d
  • 10,244
  • 7
  • 28
  • 56
user3673737
  • 35
  • 6
  • Do you have access to the Curve Fitting Toolbox? The [fit function with 'gauss2' option](https://www.mathworks.com/help/curvefit/gaussian.html#bs41yzj-1) might be easier to use. – Cecilia Aug 28 '17 at 18:56
  • Thank you for your answer. Yes, I do have it but I wish to do the fitting this way to make it a general code for future use. Currently, I am interested to learn what the issue might be. Is this to do with the solver or perhaps lsqcurvefit function isn't the best to use in this case? – user3673737 Aug 28 '17 at 19:02

1 Answers1

4

Short answer: check the stopping criteria details and change the stopping criteria accordingly:

options = optimoptions('lsqcurvefit','OptimalityTolerance', 1e-16, 'FunctionTolerance', 1e-16);
xfit = lsqcurvefit(@testfunction,[19,-4],xdata, ydata, [], [], options);

What is the problem?

lsqcurvefit is a numerical solver and therefore uses a stopping criteria to determine if the local minimum is sufficiently reached. In general, you never reach the exact solution. Therefore, the solution to your problem is to change the stopping criteria to request a more accurate solution.

How to solve it?

By clicking on stopping criteria details, you receive the following explanation:

Optimization completed: The final point is the initial point. The first-order optimality measure, 7.254593e-07, is less than options.OptimalityTolerance = 1.000000e-06.

Optimization Metric                                       Options 
relative first-order optimality =   7.25e-07  OptimalityTolerance =   1e-06 (default)

So, you should decrease the OptimalityTolerance (f.e. to 1e-16):

options = optimoptions('lsqcurvefit','OptimalityTolerance', 1e-16);
xfit = lsqcurvefit(@testfunction,[19,-4],xdata, ydata, [], [], options);

enter image description here

The above image visualizes the new result, which is better than the previous one, but not yet very good. By inspecting the stopping criteria again, you will see that you also need to change FunctionTolerance:

options = optimoptions('lsqcurvefit','OptimalityTolerance', 1e-16, 'FunctionTolerance', 1e-16);

enter image description here

Why are the default options that bad?

Note that you need to tweak the stopping criteria, because your function returns relative small values. Multiplying z with a factor of 1000, without any option specification would also result in a nice fit:

enter image description here

m7913d
  • 10,244
  • 7
  • 28
  • 56
  • Thank you very much. I didn't know that one could easily change the optimization settings. I have now a good idea what to look for in the future if I get stuck with such fitting routines. Thanks again! – user3673737 Aug 28 '17 at 20:07