I am writing web crawler scheduler and have run into problems. First I will describe how I'm trying to find optimal schedule for when my crawler is visiting the page and then I will present my problem.
Scheduler definition
Scheduler is based on this paper "Optimal crawling strategies for web search engines" by J.Wolf. The paper proposes that update times of web pages follow exponential distribution with parameter λ. The problem is finding optimal number of times xi, the page i will be crawled in time interval [0,T]. The function proposed is:

Because this function is convex and its input arguments xi is discrete this kind of problem can be solved using algorithm suggested by Fredrerickson and Johnson in "The Complexity of Selection and Ranking in X + Y and Matrices with sorted columns", that has time complexity O(max{N, log(R/N)}). The optimization algorithm solves the problem by finding N-th element in [RxN] matrix where element at position (i, j) is equal to derivation of j function with input argument x = i, where derivation dj(xi) is equal to:

Because function fi is convex that means that function di has property that is monotonically increasing (matrix has sorted columns).
Problems
I run into problems when evaluating derivation, because of rounding errors d(x+1) - d(x), did not have guarantee to be greater or equal to 0, and I'm not sure that values that I got from optimizer are optional values. Rounding errors happen because value of x can be only positive integers in range of 0 to few billions, therefor exponent in function f is either big negative number or extremely small number (-5000).
Failed Attempts
The first thing I tried, I downloaded arbitrary precision library. This solved my problem but the overhead of library is to big.
The second thing I tried was I expanded d and got function like:
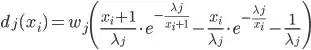
and then I tried to compare dj(xi) and dk(xw) by comparing their terms individually and than try to deduce is dj is bigger or smaller or greater than dk. If I could compare derivation I could solve my problem because optimization algorithm does not need concrete values, instead it only need relations between values. I couldn't find the solution because the term w.
I also tried looking at log(dj(xi)) because log preserves function monotony, but log also had rounding errors and I couldn't compare log(dj) and log(dk) without computing the final values.
If anybody has any other solution that could potentially work I would be most graceful.