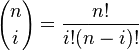I am working on a project which involves combining two Weibull distributions and thus creating a double peaked curve. I then aim to make predictions using this. I have searched online and I can't seem to find anything on this or if R has a function that allows me to combine two Weibulls. Below shows the code I have used to create the two Weibull distributions I wish to combine to make one single probability density function.
curve(dweibull(x, scale=30.59898985, shape=2.27136646),from=0, to=70, main="Weibull distribution")
curve(dweibull(x, scale=19.39743639, shape=1.22800332),from=0, to=70, main="Weibull distribution")
Any help would be amazing.
Thanks!