FFT window causing unequal amplification across frequency spectrum

Question

I am using FFTW to create a spectrum analyzer in C++.

After applying any window function to an input signal, the output amplitude suddenly seems to scale with frequency.

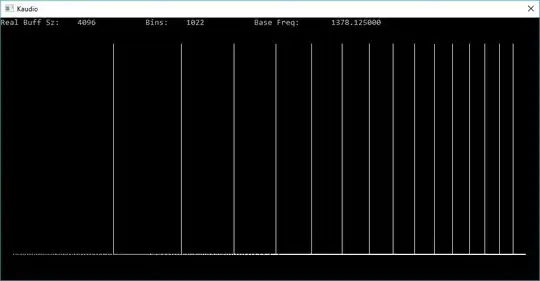
Retangular Window

Exact-Blackman

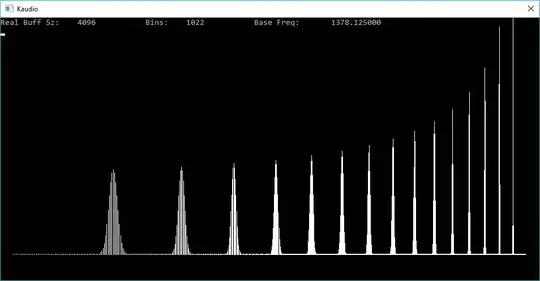
Graphs are scaled logarithmically with a sampling frequency of 44100 Hz. All harmonics are generated at the same level, peaking at 0dB as seen during the rectangular case. The Exact-Blackman window was amplified by 7.35dB to attempt to makeup for processing gain.

Here is my code for generating the input table...

freq = 1378.125f;

for (int i = 0; i < FFT_LOGICAL_SIZE; i++)
{
    float term = 2 * PI * i / FFT_ORDER;

    for (int h = 1; freq * h < FREQ_NYQST; h+=1) // Harmonics up to Nyquist
    {
        fftInput[i] += sinf(freq * h * K_PI * i / K_SAMPLE_RATE); // Generate sine
        fftInput[i] *= (7938 / 18608.f) - ((9240 / 18608.f) * cosf(term)) + ((1430 / 18608.f) * cosf(term * 2)); // Exact-Blackman window
    }
}

fftwf_execute(fftwR2CPlan);

Increasing or decreasing the window size changes nothing. I tested with the Hamming window as well, same problem.

Here is my code for grabbing the output.

float val; // Used elsewhere
for (int i = 1; i < K_FFT_COMPLEX_BINS_NOLAST; i++) // Skips the DC and Nyquist bins
{
    real = fftOutput[i][0];
    complex = fftOutput[i][1];

    // Grabs the values and scales based on the window size
    val = sqrtf(real * real + complex * complex) / FFT_LOGICAL_SIZE_OVER_2;
    val *= powf(20, 7.35f / 20); // Only applied during Exact-Blackman test
}

Curiously, I attempted the following to try to flatten out the response in the Exact-Blackman case. This scaling back down resulted in a nearly, but still not perfectly flat response. Neat, but still doesn't explain to me why this is happening.

float x = (float)(FFT_COMPLEX_BINS - i) / FFT_COMPLEX_BINS; // Linear from 0 to 1
x = log10f((x * 9) + 1.3591409f); // Now logarithmic from 0 to 1, offset by half of Euler's constant
val = sqrt(real * real + complex * complex) / (FFT_LOGICAL_SIZE_OVER_2 / x); // Division by x added to this line

score 1 · Accepted Answer · answered Aug 06 '17 at 16:50

1

Might be a bug. You seem to be applying your window function multiple times per sample. Any windowing should be removed from your input compositing loop and applied to the input vector just once, right before the FFT.

answered Aug 06 '17 at 16:50

hotpaw2

70,107
14
90
153

Well spotted! This was it! Thanks so much! – Krunklehorn Aug 07 '17 at 17:27

score 0 · Answer 2 · answered Aug 05 '17 at 23:25

I was not able to reproduce code because I do not have the library on hand. However, This may be a consequence of spectral leakage. https://en.wikipedia.org/wiki/Spectral_leakage

This is an inevevitiblity of window functions as well as sampling. If you look at the tradeoffs section of that article, the type of window can be adaptive for a wide range of frequencies or focused on a particular one. Since the frequency of your signal is increasing perhaps the lower freq signal outside your target is more subjected to spectral leakage.

FFT window causing unequal amplification across frequency spectrum

2 Answers2