I'm trying to use Modelica for modeling of a system composed of elastic pipes. For now, I'm trying to implement my own dynamic pipe model (rigid, not yet elastic) using the same approach (finite volume, staggered) like in the Modelica.Fluid library, but of course not including all the options.
This model should be more simple to understand, as it's a flat model, not extending from other classes. This is important because therefore my colleagues can understand the model even without Modelica Knowhow and I can convince them that Modelica is the adequate tool for our purposes!
As a test case I use a mass flow source with a step signal (waterhammer). My model gives not the same results like the Modelica.Fluid component. I would really appreciate, if somebody can help me, understand what's happening!
The test system looks like this:
The results for 11 cells are this:
As you can see, the pressure peak is higher for the MSL component and the frequency/period is not the same. When I chose more cells then the error gets smaller.
I'm quite sure that I'm using exactly the same equations. Could it be cause of numerical reasons (I tryied using nominal values)? I also included my own "fixed zeta" flow model for the Modelica.Fluid component so I can compare it in case of a fixed pressure loss coefficient zeta.
The code of my pipe model is quite short and it would be really nice if I get it to work like this:
model Pipe_FVM_staggered
// Import
import SI = Modelica.SIunits;
import Modelica.Constants.pi;
// Medium
replaceable package Medium = Modelica.Media.Interfaces.PartialMedium "Medium in the component"
annotation (choicesAllMatching = true);
// Interfaces, Ports
Modelica.Fluid.Interfaces.FluidPort_a port_a(redeclare package Medium = Medium) annotation (Placement(transformation(extent={{-110,-10},{-90,10}})));
Modelica.Fluid.Interfaces.FluidPort_b port_b(redeclare package Medium = Medium) annotation (Placement(transformation(extent={{90,-10},{110,10}})));
// Parameters
parameter Integer n(min=2) = 3 "Number of cells"; // No effect yet, only for icon
parameter SI.Length L = 1 "Length";
parameter SI.Diameter D = 0.010 "Diameter";
parameter SI.Height R = 2.5e-5 "Roughness";
parameter Boolean use_fixed_zeta = false "Use fixed zeta value instead of Moody chart";
parameter SI.CoefficientOfFriction zeta = 1;
// Initialization
parameter Medium.Temperature T_start = 293.15 "Start temperature" annotation(Dialog(tab="Initialization"));
parameter Medium.MassFlowRate mflow_start = 1 "Start mass flow rate in design direction" annotation(Dialog(tab="Initialization"));
parameter Medium.AbsolutePressure p_a_start = 2e5 "Start pressure p[1] at design inflow" annotation(Dialog(tab="Initialization"));
parameter Medium.AbsolutePressure p_b_start = 1e5 "Start pressure for p[n+1] at design outflow" annotation(Dialog(tab="Initialization"));
// parameter Medium.AbsolutePressure p_start = (p_a_start + p_b_start)/2 annotation(Dialog(tab="Initialization"));
parameter Medium.AbsolutePressure p_start[:] = linspace(p_a_start, p_b_start, n) annotation(Dialog(tab="Initialization"));
// parameter Medium.SpecificEnthalpy h_start[:] = Medium.specificEnthalpy_pTX(p_start, T_start, Medium.X_default);
parameter Medium.SpecificEnthalpy h_start = Medium.specificEnthalpy_pTX((p_a_start + p_b_start)/2, T_start, Medium.X_default) annotation(Dialog(tab="Initialization"));
parameter SI.AbsolutePressure dp_nominal = 1e5;
parameter SI.MassFlowRate m_flow_nominal = 1;
// Variables general
SI.Length dL = L/n;
SI.Area A(nominal=0.001) = D^2*pi/4;
SI.Volume V = A * dL;
// Variables cell centers: positiv in direction a -> b
Medium.AbsolutePressure p[n](start = p_start, each stateSelect=StateSelect.prefer) annotation(Dialog(tab="Initialization", showStartAttribute=true, enable=false));
Medium.SpecificEnthalpy h[n](each start = h_start, each stateSelect=StateSelect.prefer) annotation(Dialog(tab="Initialization", showStartAttribute=true, enable=false));
Medium.ThermodynamicState state[n] = Medium.setState_phX(p,h);
SI.Mass m[n] = rho .* V;
Medium.Density rho[n] = Medium.density(state);
SI.InternalEnergy U[n] = m .* u;
Medium.SpecificInternalEnergy u[n] = Medium.specificInternalEnergy(state);
Medium.Temperature T[n] = Medium.temperature(state);
Medium.DynamicViscosity mu[n] = Medium.dynamicViscosity(state);
SI.Velocity v[n](nominal=0.2) = 0.5 * (mflow[1:n] + mflow[2:n+1]) ./ rho ./ A;
SI.Power Wflow[n];
SI.MomentumFlux Iflow[n] = v .* v .* rho * A;
// Variables faces: positiv in direction a -> b
Medium.MassFlowRate mflow[n+1](each start = mflow_start, each stateSelect=StateSelect.prefer, nominal=0.25) annotation(Dialog(tab="Initialization", showStartAttribute=true, enable=false));
Medium.EnthalpyFlowRate Hflow[n+1];
SI.Momentum I[n-1] = mflow[2:n] * dL;
SI.Force Fp[n-1];
SI.Force Ff[n-1];
SI.PressureDifference dpf[n-1](each start = (p_a_start - p_b_start)/(n-1), nominal=0.01e5) annotation(Dialog(tab="Initialization", showStartAttribute=true, enable=false));
equation
der(m) = mflow[1:n] - mflow[2:n+1]; // Mass balance
der(U) = Hflow[1:n] - Hflow[2:n+1] + Wflow; // Energy balance
der(I) = Iflow[1:n-1] - Iflow[2:n] + Fp - Ff; // Momentum balance, staggered
Hflow[1] = semiLinear(mflow[1], inStream(port_a.h_outflow), h[1]);
Hflow[2:n] = semiLinear(mflow[2:n], h[1:n-1], h[2:n]);
Hflow[n+1] = semiLinear(mflow[n+1], h[n], inStream(port_b.h_outflow));
Wflow[1] = v[1] * A .* ( (p[2] - p[1])/2 + dpf[1]/2);
Wflow[2:n-1] = v[2:n-1] * A .* ( (p[3:n]-p[1:n-2])/2 + (dpf[1:n-2]+dpf[2:n-1])/2);
Wflow[n] = v[n] * A .* ( (p[n] - p[n-1])/2 + dpf[n-1]/2);
Fp = A * (p[1:n-1] - p[2:n]);
Ff = A * dpf; // dpf = Ff ./ A;
if use_fixed_zeta then
dpf = 1/2 * zeta/(n-1) * (mflow[2:n]).^2 ./ ( 0.5*(rho[1:n-1] + rho[2:n]) * A * A);
else
dpf = homotopy(
actual = Modelica.Fluid.Pipes.BaseClasses.WallFriction.Detailed.pressureLoss_m_flow(
m_flow = mflow[2:n],
rho_a = rho[1:n-1],
rho_b = rho[2:n],
mu_a = mu[1:n-1],
mu_b = mu[2:n],
length = dL,
diameter = D,
roughness = R,
m_flow_small = 0.001),
simplified = dp_nominal/(n-1)/m_flow_nominal*mflow[2:n]);
end if;
// Boundary conditions
mflow[1] = port_a.m_flow;
mflow[n] = -port_b.m_flow;
p[1] = port_a.p;
p[n] = port_b.p;
port_a.h_outflow = h[1];
port_b.h_outflow = h[n];
initial equation
der(mflow[2:n]) = zeros(n-1);
der(p) = zeros(n);
der(h) = zeros(n);
annotation (Icon(coordinateSystem(preserveAspectRatio=false), graphics={Rectangle(
extent={{-100,60},{100,-60}},
fillColor={255,255,255},
fillPattern=FillPattern.HorizontalCylinder,
lineColor={0,0,0}),
Line(
points={{-100,60},{-100,-60}},
color={0,0,0},
thickness=0.5),
Line(
points={{-60,60},{-60,-60}},
color={0,0,0},
thickness=0.5),
Line(
points={{-20,60},{-20,-60}},
color={0,0,0},
thickness=0.5),
Line(
points={{20,60},{20,-60}},
color={0,0,0},
thickness=0.5),
Line(
points={{60,60},{60,-60}},
color={0,0,0},
thickness=0.5),
Line(
points={{100,60},{100,-60}},
color={0,0,0},
thickness=0.5),
Line(
points={{60,-80},{-60,-80}},
color={0,128,255},
visible=showDesignFlowDirection),
Polygon(
points={{20,-65},{60,-80},{20,-95},{20,-65}},
lineColor={0,128,255},
fillColor={0,128,255},
fillPattern=FillPattern.Solid,
visible=showDesignFlowDirection),
Text(
extent={{-150,100},{150,60}},
lineColor={0,0,255},
textString="%name"),
Text(
extent={{-40,22},{40,-18}},
lineColor={0,0,0},
textString="n = %n")}), Diagram(
coordinateSystem(preserveAspectRatio=false)));
end Pipe_FVM_staggered;
I'm struggling with this problem since quite a long time, so any comments or hints are really appreciated!! If you need some more information or test results, please tell me!
This is the code for the test example:
model Test_Waterhammer
extends Modelica.Icons.Example;
import SI = Modelica.SIunits;
import g = Modelica.Constants.g_n;
replaceable package Medium = Modelica.Media.Water.StandardWater;
Modelica.Fluid.Sources.Boundary_pT outlet(
redeclare package Medium = Medium,
nPorts=1,
p=2000000,
T=293.15)
annotation (Placement(transformation(extent={{90,-10},{70,10}})));
inner Modelica.Fluid.System system(
allowFlowReversal=true,
energyDynamics=Modelica.Fluid.Types.Dynamics.SteadyStateInitial,
massDynamics=Modelica.Fluid.Types.Dynamics.SteadyStateInitial,
momentumDynamics=Modelica.Fluid.Types.Dynamics.SteadyStateInitial,
m_flow_start=0.1,
m_flow_small=0.0001)
annotation (Placement(transformation(extent={{60,60},{80,80}})));
Modelica.Fluid.Sources.MassFlowSource_T inlet(
redeclare package Medium = Medium,
nPorts=1,
m_flow=0.1,
use_m_flow_in=true,
T=293.15)
annotation (Placement(transformation(extent={{-50,-10},{-30,10}})));
Modelica.Blocks.Sources.TimeTable timeTable(table=[0,0.1; 1,0.1; 1,0.25;
40,0.25; 40,0.35; 60,0.35])
annotation (Placement(transformation(extent={{-90,10},{-70,30}})));
Pipe_FVM_staggered pipe(
redeclare package Medium = Medium,
R=0.035*0.005,
mflow_start=0.1,
L=1000,
m_flow_nominal=0.1,
D=0.035,
zeta=2000,
n=11,
use_fixed_zeta=false,
T_start=293.15,
p_a_start=2010000,
p_b_start=2000000,
dp_nominal=10000)
annotation (Placement(transformation(extent={{10,-10},{30,10}})));
Modelica.Fluid.Pipes.DynamicPipe pipeMSL(
redeclare package Medium = Medium,
allowFlowReversal=true,
length=1000,
roughness=0.035*0.005,
m_flow_start=0.1,
energyDynamics=Modelica.Fluid.Types.Dynamics.SteadyStateInitial,
massDynamics=Modelica.Fluid.Types.Dynamics.SteadyStateInitial,
momentumDynamics=Modelica.Fluid.Types.Dynamics.SteadyStateInitial,
diameter=0.035,
modelStructure=Modelica.Fluid.Types.ModelStructure.av_vb,
redeclare model FlowModel =
Modelica.Fluid.Pipes.BaseClasses.FlowModels.DetailedPipeFlow (
useUpstreamScheme=false, use_Ib_flows=true),
p_a_start=2010000,
p_b_start=2000000,
T_start=293.15,
nNodes=11)
annotation (Placement(transformation(extent={{10,-50},{30,-30}})));
Modelica.Fluid.Sources.MassFlowSource_T inlet1(
redeclare package Medium = Medium,
nPorts=1,
m_flow=0.1,
use_m_flow_in=true,
T=293.15)
annotation (Placement(transformation(extent={{-48,-50},{-28,-30}})));
Modelica.Fluid.Sources.Boundary_pT outlet1(
redeclare package Medium = Medium,
nPorts=1,
p=2000000,
T=293.15)
annotation (Placement(transformation(extent={{90,-50},{70,-30}})));
equation
connect(inlet.ports[1], pipe.port_a)
annotation (Line(points={{-30,0},{-10,0},{10,0}}, color={0,127,255}));
connect(pipe.port_b, outlet.ports[1])
annotation (Line(points={{30,0},{50,0},{70,0}}, color={0,127,255}));
connect(inlet1.ports[1], pipeMSL.port_a)
annotation (Line(points={{-28,-40},{-10,-40},{10,-40}}, color={0,127,255}));
connect(pipeMSL.port_b, outlet1.ports[1])
annotation (Line(points={{30,-40},{50,-40},{70,-40}}, color={0,127,255}));
connect(timeTable.y, inlet.m_flow_in)
annotation (Line(points={{-69,20},{-60,20},{-60,8},{-50,8}}, color={0,0,127}));
connect(inlet1.m_flow_in, inlet.m_flow_in)
annotation (Line(points={{-48,-32},{-60,-32},{-60,8},{-50,8}}, color={0,0,127}));
annotation (Icon(coordinateSystem(preserveAspectRatio=false)), Diagram(
coordinateSystem(preserveAspectRatio=false)),
experiment(
StopTime=15,
__Dymola_NumberOfIntervals=6000,
Tolerance=1e-005,
__Dymola_Algorithm="Dassl"));
end Test_Waterhammer;
I've run the test with 301 cells:
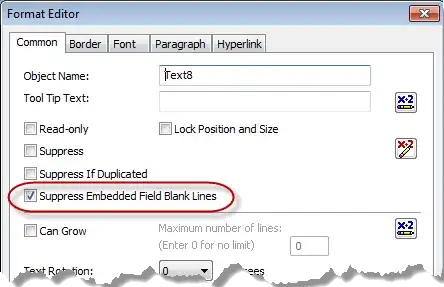
Solution: Modifications as suggested by scottG
model FVM_staggered_Ncells
// Import
import SI = Modelica.SIunits;
import Modelica.Constants.pi;
// Medium
replaceable package Medium = Modelica.Media.Interfaces.PartialMedium "Medium in the component"
annotation (choicesAllMatching = true);
// Interfaces, Ports
Modelica.Fluid.Interfaces.FluidPort_a port_a(redeclare package Medium = Medium) annotation (Placement(transformation(extent={{-110,-10},{-90,10}})));
Modelica.Fluid.Interfaces.FluidPort_b port_b(redeclare package Medium = Medium) annotation (Placement(transformation(extent={{90,-10},{110,10}})));
// Parameters
parameter Integer n(min=2) = 3 "Number of cells"; // No effect yet, only for icon
parameter SI.Length L = 1 "Length";
parameter SI.Diameter D = 0.010 "Diameter";
parameter SI.Height R = 2.5e-5 "Roughness";
parameter Boolean use_fixed_zeta = false "Use fixed zeta value instead of Moody chart";
parameter SI.CoefficientOfFriction zeta = 1;
// Initialization
parameter Medium.Temperature T_start = 293.15 "Start temperature" annotation(Dialog(tab="Initialization"));
parameter Medium.MassFlowRate mflow_start = 1 "Start mass flow rate in design direction" annotation(Dialog(tab="Initialization"));
parameter Medium.AbsolutePressure p_a_start = 2e5 "Start pressure p[1] at design inflow" annotation(Dialog(tab="Initialization"));
parameter Medium.AbsolutePressure p_b_start = 1e5 "Start pressure for p[n+1] at design outflow" annotation(Dialog(tab="Initialization"));
parameter Medium.AbsolutePressure p_start[:] = linspace(p_a_start, p_b_start, n) annotation(Dialog(tab="Initialization"));
// parameter Medium.SpecificEnthalpy h_start[:] = Medium.specificEnthalpy_pTX(p_start, T_start, Medium.X_default);
parameter Medium.SpecificEnthalpy h_start = Medium.specificEnthalpy_pTX((p_a_start + p_b_start)/2, T_start, Medium.X_default) annotation(Dialog(tab="Initialization"));
parameter SI.AbsolutePressure dp_nominal = 1e5;
parameter SI.MassFlowRate m_flow_nominal = 1;
// Variables general
SI.Length dL = L/n;
SI.Length dLs[n-1] = cat(1,{1.5*dL}, fill(dL,n-3), {1.5*dL});
SI.Area A = D^2*pi/4;
SI.Volume V = A * dL;
// Variables cell centers: positiv in direction a -> b
Medium.AbsolutePressure p[n](start = p_start, each stateSelect=StateSelect.prefer) annotation(Dialog(tab="Initialization", showStartAttribute=true, enable=false));
Medium.SpecificEnthalpy h[n](each start = h_start, each stateSelect=StateSelect.prefer) annotation(Dialog(tab="Initialization", showStartAttribute=true, enable=false));
Medium.ThermodynamicState state[n] = Medium.setState_phX(p,h);
SI.Mass m[n] = rho .* V;
Medium.Density rho[n] = Medium.density(state);
SI.InternalEnergy U[n] = m .* u;
Medium.SpecificInternalEnergy u[n] = Medium.specificInternalEnergy(state);
Medium.Temperature T[n] = Medium.temperature(state);
Medium.DynamicViscosity mu[n] = Medium.dynamicViscosity(state);
SI.Velocity v[n] = 0.5 * (mflow[1:n] + mflow[2:n+1]) ./ rho ./ A;
SI.Power Wflow[n];
SI.MomentumFlux Iflow[n] = v .* v .* rho * A;
// Variables faces: positiv in direction a -> b
Medium.MassFlowRate mflow[n+1](each start = mflow_start, each stateSelect=StateSelect.prefer) annotation(Dialog(tab="Initialization", showStartAttribute=true, enable=false));
Medium.EnthalpyFlowRate Hflow[n+1];
SI.Momentum I[n-1] = mflow[2:n] .* dLs;
SI.Force Fp[n-1];
SI.Force Ff[n-1];
SI.PressureDifference dpf[n-1](each start = (p_a_start - p_b_start)/(n-1)) annotation(Dialog(tab="Initialization", showStartAttribute=true, enable=false));
equation
der(m) = mflow[1:n] - mflow[2:n+1]; // Mass balance
der(U) = Hflow[1:n] - Hflow[2:n+1] + Wflow; // Energy balance
der(I) = Iflow[1:n-1] - Iflow[2:n] + Fp - Ff; // Momentum balance, staggered
Hflow[1] = semiLinear(mflow[1], inStream(port_a.h_outflow), h[1]);
Hflow[2:n] = semiLinear(mflow[2:n], h[1:n-1], h[2:n]);
Hflow[n+1] = semiLinear(mflow[n+1], h[n], inStream(port_b.h_outflow));
Wflow[1] = v[1] * A .* ( (p[2] - p[1])/2 + dpf[1]/2);
Wflow[2:n-1] = v[2:n-1] * A .* ( (p[3:n]-p[1:n-2])/2 + (dpf[1:n-2]+dpf[2:n-1])/2);
Wflow[n] = v[n] * A .* ( (p[n] - p[n-1])/2 + dpf[n-1]/2);
Fp = A * (p[1:n-1] - p[2:n]);
Ff = A * dpf;
if use_fixed_zeta then
dpf = 0.5 * zeta/(n-1) * abs(mflow[2:n]) .* mflow[2:n] ./ ( 0.5*(rho[1:n-1] + rho[2:n]) * A * A);
else
dpf = homotopy(
actual = Modelica.Fluid.Pipes.BaseClasses.WallFriction.Detailed.pressureLoss_m_flow(
m_flow = mflow[2:n],
rho_a = 0.5*(rho[1:n-1] + rho[2:n]),
rho_b = 0.5*(rho[1:n-1] + rho[2:n]),
mu_a = 0.5*(mu[1:n-1] + mu[2:n]),
mu_b = 0.5*(mu[1:n-1] + mu[2:n]),
length = dLs,
diameter = D,
roughness = R,
m_flow_small = 0.001),
simplified = dp_nominal/(n-1)/m_flow_nominal*mflow[2:n]);
end if;
// Boundary conditions
mflow[1] = port_a.m_flow;
mflow[n+1] = -port_b.m_flow;
p[1] = port_a.p;
p[n] = port_b.p;
port_a.h_outflow = h[1];
port_b.h_outflow = h[n];
initial equation
der(mflow[2:n]) = zeros(n-1);
der(p) = zeros(n);
der(h) = zeros(n);
annotation (Icon(coordinateSystem(preserveAspectRatio=false), graphics={Rectangle(
extent={{-100,60},{100,-60}},
fillColor={255,255,255},
fillPattern=FillPattern.HorizontalCylinder,
lineColor={0,0,0}),
Line(
points={{-100,60},{-100,-60}},
color={0,0,0},
thickness=0.5),
Line(
points={{-60,60},{-60,-60}},
color={0,0,0},
thickness=0.5),
Line(
points={{-20,60},{-20,-60}},
color={0,0,0},
thickness=0.5),
Line(
points={{20,60},{20,-60}},
color={0,0,0},
thickness=0.5),
Line(
points={{60,60},{60,-60}},
color={0,0,0},
thickness=0.5),
Line(
points={{100,60},{100,-60}},
color={0,0,0},
thickness=0.5),
Line(
points={{60,-80},{-60,-80}},
color={0,128,255},
visible=showDesignFlowDirection),
Polygon(
points={{20,-65},{60,-80},{20,-95},{20,-65}},
lineColor={0,128,255},
fillColor={0,128,255},
fillPattern=FillPattern.Solid,
visible=showDesignFlowDirection),
Text(
extent={{-150,100},{150,60}},
lineColor={0,0,255},
textString="%name"),
Text(
extent={{-40,22},{40,-18}},
lineColor={0,0,0},
textString="n = %n")}),
Diagram(coordinateSystem(preserveAspectRatio=false)));
end FVM_staggered_Ncells;