You can choose any function approximator that is differentiable.
Two commonly used classes of value function approximators are:
Linear function approximators: Linear combinations of features
For approximating Q (the action-value)
1. Find features that are functions of states and actions.
2. Represent q as a weighted combination of these features.
where  is a vector in
is a vector in  with
with  component given by
component given by  and
and  is the weight vector
is the weight vector 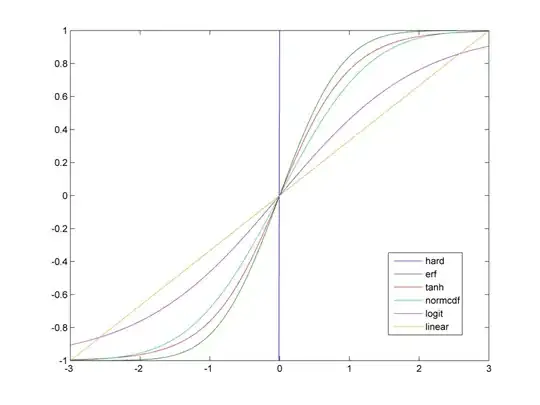 whose
whose  componenet is given by
componenet is given by  .
.
Neural Network
Represent  using a neural network. You can either approximate using action-in (left of figure below) type or action-out (right of figure below) type. The difference being that the neural network can either take as input representations of both the state and the action and produce a single value (Q-value) as the output or take as input only the representation of state
using a neural network. You can either approximate using action-in (left of figure below) type or action-out (right of figure below) type. The difference being that the neural network can either take as input representations of both the state and the action and produce a single value (Q-value) as the output or take as input only the representation of state s and provide as output one value for each action, a in the action space (This type is easier to realize if the action space is discrete and finite).
Using the first type (action-in) for the example as it is close to the example in the linear case, you could create a Q-value approximator using a neural network with the following approach:
Represent the state-action value as a normalized vector
(or as a one-hot vector representing the state and action)
1. Input layer : Size= number of inputs
2. `n` hidden layers with `m` neurons
3. Output layer: single output neuron
Sigmoid activation function.
Update weights using gradient descent as per the * semi-gradient Sarsa algorithm*.
You could also directly use the visuals (if available) as the input and use convolutional layers like in the DQN paper. But read the note below regarding the convergence and additional tricks to stabilize such non-linear approximator based method.
Graphically the function approximator looks like this:

Note that  is an elementary function and
is an elementary function and  is used to represent elements of the state-action vector.
You can use any elementary function in place of
is used to represent elements of the state-action vector.
You can use any elementary function in place of  . Some common ones are linear regressors, Radial Basis Functions etc.
. Some common ones are linear regressors, Radial Basis Functions etc.
A good differentiable function depends on the context. But in reinforcement learning settings, convergence properties and the error bounds are important. The Episodic semi-gradient Sarsa algorithm discussed in the book has similar convergence properties as of TD(0) for a constant policy.
Since you specifically asked for on-policy prediction, using a linear function approximator is advisable to use because it is guaranteed to converge. The following are some of the other properties that make the Linear function approximators suitable:
- The error surface becomes a quadratic surface with a single minimum with mean square error function. This makes it a sure-shot solution as gradient descent is guaranteed to find the minima which is the global optimum.
The error bound (as proved by Tsitsiklis & Roy,1997 for the general case of TD(lambda) ) is:
Which means that the asymptotic error will be no more than  times the smallest possible error. Where
times the smallest possible error. Where  is the discount factor.
The gradient is simple to calculate!
is the discount factor.
The gradient is simple to calculate!
Using a non-linear approximator (like a (deep) neural network) however does not inherently guarantee convergence.
Gradient TD method uses the true gradient of the projected bellman error for the updates instead of the semi-gradient used in the Episodic semi-gradient Sarsa algorithm which is known to provide convergence even with non-linear function approximators (even for off-policy prediction) if certain conditions are met.
 ? Are there any standard strategies to choose it?
? Are there any standard strategies to choose it?
















