3

After numerically solving a differential equation and plotting the results I would like to determine the single maximum value in the plotted range but do not know how.

The code below works for numerically solving the differential equation and plotting the results.

s = NDSolve[{x''[t] + x[t] - 0.167 x[t]^3 == 0.005 Cos[t + -0.0000977162*t^2/2], x[0] == 0, x'[0] == 0}, x, {t, 0, 1000}]

Plot[Evaluate[x[t] /. s], {t, 0, 1000}, 
Frame -> {True, True, False, False}, FrameLabel -> {"t", "x"}, FrameStyle -> Directive[FontSize -> 15], Axes -> False]

Mathematica graphics

Sjoerd C. de Vries
  • 16,122
  • 3
  • 42
  • 94
Carey
  • 1,137
  • 3
  • 11
  • 18

2 Answers2

4

Use NMaximize

First approximation: 

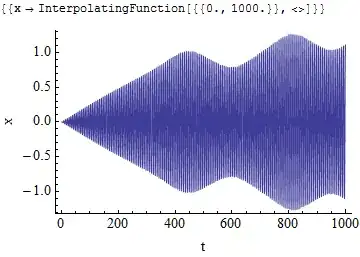
s = NDSolve[{x''[t] + x[t] - 0.167 x[t]^3 ==  
            0.005 Cos[t + -0.0000977162*t^2/2], x[0] == 0, x'[0] == 0}, x[t], 
            {t, 0, 1000}]
NMaximize[{Evaluate[x[t] /. s[[1]]] , 100 < t < 1000}, t]  

{1.26625, {t -> 821.674}}

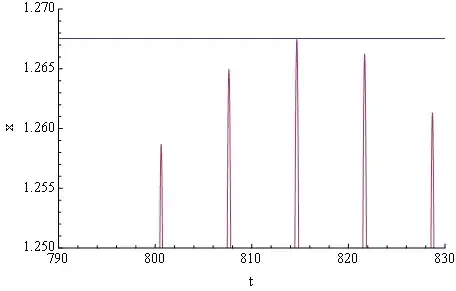
As your function is a rapid oscillation like this : alt text , it doesn't catch the real max value, as you may see below: 

Plot[{1.26625, Evaluate[x[t] /. s[[1]]]}, {t, 790, 830}, 
 Frame -> {True, True, False, False}, FrameLabel -> {"t", "x"}, 
 FrameStyle -> Directive[FontSize -> 15], Axes -> False, 
 PlotRange -> {{790, 830}, {1.25, 1.27}}]

alt text

So we refine our bounds, and tune a little the NMaximize function: 

NMaximize[{Evaluate[x[t] /. s[[1]]] , 814 < t < 816}, t, 
 AccuracyGoal -> 20, PrecisionGoal -> 18, MaxIterations -> 1000]  

NMaximize::cvmit: Failed to converge to the requested accuracy or 
                  precision within 1000 iterations. >>

{1.26753, {t -> 814.653}}

It failed to converge within the required accuracy, but now the result is good enough

Plot[{1.2675307922753962`, Evaluate[x[t] /. s[[1]]]}, {t, 790, 830}, 
 Frame -> {True, True, False, False}, FrameLabel -> {"t", "x"}, 
 FrameStyle -> Directive[FontSize -> 15], Axes -> False, 
 PlotRange -> {{790, 830}, {1.25, 1.27}}]

alt text

Dr. belisarius
  • 60,527
  • 15
  • 115
  • 190
  • Any reason why you don't like `FindMaximum[]`? :) –  Dec 25 '10 at 02:45
  • @J. M. Because NMaximize attempts to find a GLOBAL maximum, while FindMaximum works well for LOCAL extremes. For an oscillating function NMaximize works better for me. See for example here http://reference.wolfram.com/mathematica/ref/FindMaximum.html the first example under **Basic Examples** – Dr. belisarius Dec 25 '10 at 20:12
  • @J. M. Could have used FindMaximum[] the second time, though. – Dr. belisarius Dec 27 '10 at 01:58
  • Well, it's a *univariate* function, and one would certainly plot the thing before trying to find roots or optima, right? I say this because bringing in the machinery of `NMaximize[]` (Nelder-Mead by default) is a bit wasteful in the univariate case, when the methods of `FindMaximum[]` are adequate. The reason for plotting before optimizing of course is that these iterative methods tend to go astray if not given a good starting point (i.e., GIGO). –  Dec 27 '10 at 03:14
  • @J. M. With rapid oscillating functions, _sometimes_ I found Plot[] deceiving. That's why I usually give a try to NMaximize. As for the _wasteful_ part, I don't agree ... as while it's running I get my share of coffee :) – Dr. belisarius Dec 27 '10 at 03:26
  • If you know in advance that your function of interest is oscillatory, it's a good idea to decrease `MaxBend` and increase `PlotDivision` . In any event... to each his own, I suppose. –  Dec 28 '10 at 04:38
  • @J. M. PlotDivision is deprecated since v6 (now is MaxRecursion). MaxBend seems also deprecated, but I'm not able to find the new Option. – Dr. belisarius Dec 28 '10 at 04:46
  • @J. M. This answer by @Yaroslav explains extensively why I don't trust Plot with rapid oscillating functions. That's a great answer, BTW http://stackoverflow.com/questions/4572183/strange-sinx-graph-in-mathematica/4572266#4572266 – Dr. belisarius Jan 01 '11 at 06:24
3

You can use Reap and Sow to extract a list of values from any evaluation. For a simple Plot you would Sow the value of the function you are plotting and enclose the entire plot in a Reap:

list = Reap[
          Plot[Sow@Evaluate[x[t] /. s], {t, 0, 1000}, 
          Frame -> {True, True, False, False},
          FrameLabel -> {"t", "x"}, 
          FrameStyle -> Directive[FontSize -> 15],
          Axes -> False]];

The first element of list is the plot itself and the second element is the list of x-values Mathematica used in the plot. To get the Maximum:

In[1]  := Max[lst[[2, 1]]]
Out[1] := 1.26191
Timo
  • 4,246
  • 6
  • 29
  • 42