On Xorshift random number generator algorithm

Question

Following is a basic implementation of the Xorshift RNG (copied from the Wikipedia):

uint32_t xor128(void) {
  static uint32_t x = 123456789;
  static uint32_t y = 362436069;
  static uint32_t z = 521288629;
  static uint32_t w = 88675123;
  uint32_t t;

  t = x ^ (x << 11);
  x = y; y = z; z = w;
  return w = w ^ (w >> 19) ^ (t ^ (t >> 8));
}

I understand that w is the returned value and x, y and z are the state ("memory") variables. However, I can't understand the purpose of more than one memory variable. Can anyone explain me this point?

Also, I tried to copy the above code to Python:

class R2:
    def __init__(self):
        self.x = x = 123456789
        self.y = 362436069
        self.z = 521288629
        self.w = 88675123
    def __call__(self):
        t = self.x ^ (self.x<<11)
        self.x = self.y
        self.y = self.z
        self.z = self.w
        w = self.w
        self.w = w ^ (w >> 19) ^(t ^ (t >> 8))
        return self.w

Then, I have generated 100 numbers and plotted their log10 values:

r2 = R2()
x2 = [math.log10(r2()) for _ in range(100)]
plot(x2, '.g')

Here is the output of the plot:

plot

And this what happens when 10000 (and not 100) numbers are generated: plot

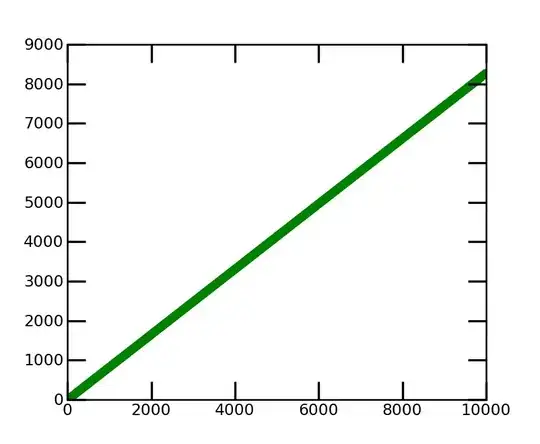
The overall tendency is very clear. And don't forget that the Y axis is log10 of the actual value.

Pretty strange behavior, don't you think?

The log10 output should've been your clue, log10 of max 32-bit is 9.something, not 100. — Lasse V. Karlsen, Dec 22 '10 at 11:52

score 18 · Accepted Answer · answered Dec 22 '10 at 11:42

The problem here is of course that you're using Python to do this.

Python has a notion of big integers, so even though you are copying an implementation that deals with 32-bit numbers, Python just says "I'll just go ahead and keep everything for you".

If you try this instead:

x2 = [r2() for _ in range(100)]
print(x2);

You'll notice that it produces ever-longer numbers, for instance here's the first number:

252977563114

and here's the last:

8735276851455609928450146337670748382228073854835405969246191481699954934702447147582960645

Here's code that has been fixed to handle this:

...
def __call__(self):
    t = self.x ^ (self.x<<11) & 0xffffffff                   # <-- keep 32 bits
    self.x = self.y
    self.y = self.z
    self.z = self.w
    w = self.w
    self.w = (w ^ (w >> 19) ^(t ^ (t >> 8))) & 0xffffffff    # <-- keep 32 bits
    return self.w
...

Aristide · Answer 2 · 2013-06-09T21:59:31.673

4

And with a generator:

def xor128():
  x = 123456789
  y = 362436069
  z = 521288629
  w = 88675123
  while True:
    t = (x ^ (x<<11)) & 0xffffffff
    (x,y,z) = (y,z,w)
    w = (w ^ (w >> 19) ^ (t ^ (t >> 8))) & 0xffffffff
    yield w

edited Jun 09 '13 at 21:59

answered Jun 09 '13 at 21:51

Aristide

3,606
2
30
50

score 2 · Answer 3 · answered Dec 22 '10 at 10:10

"However, I can't understand the purpose of more than one memory variable" - if you need to 'remember' 128 bits then you need 4 x 32bit integers.

As to the very strange distribution of 100 randoms, no idea! I could understand perhaps if you had generated a few million, and the steps in the graph were artifacts, but not 100.

On Xorshift random number generator algorithm

3 Answers3