Vector math, finding coördinates on a planar between 2 vectors

Question

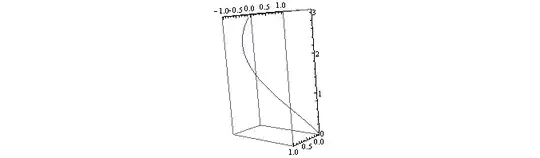
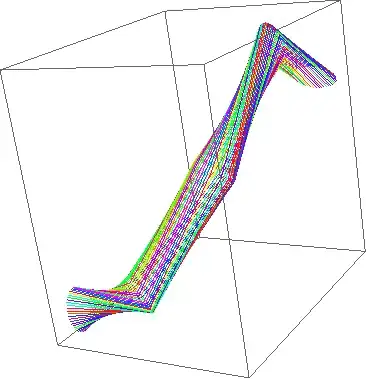
I am trying to generate a 3d tube along a spline. I have the coördinates of the spline (x1,y1,z1 - x2,y2,z2 - etc) which you can see in the illustration in yellow. At those points I need to generate circles, whose vertices are to be connected at a later stadium. The circles need to be perpendicular to the 'corners' of two line segments of the spline to form a correct tube. Note that the segments are kept low for illustration purpose.

[apparently I'm not allowed to post images so please view the image at this link] http://img191.imageshack.us/img191/6863/18720019.jpg

I am as far as being able to calculate the vertices of each ring at each point of the spline, but they are all on the same planar ie same angled. I need them to be rotated according to their 'legs' (which A & B are to C for instance).

I've been thinking this over and thought of the following:

• two line segments can be seen as 2 vectors (in illustration A & B)
• the corner (in illustraton C) is where a ring of vertices need to be calculated
• I need to find the planar on which all of the vertices will reside
• I then can use this planar (=vector?) to calculate new vectors from the center point, which is C
• and find their x,y,z using radius * sin and cos

However, I'm really confused on the math part of this. I read about the dot product but that returns a scalar which I don't know how to apply in this case.

Can someone point me into the right direction?

[edit] To give a bit more info on the situation:

I need to construct a buffer of floats, which -in groups of 3- describe vertex positions and will be connected by OpenGL ES, given another buffer with indices to form polygons.

To give shape to the tube, I first created an array of floats, which -in groups of 3- describe control points in 3d space.

Then along with a variable for segment density, I pass these control points to a function that uses these control points to create a CatmullRom spline and returns this in the form of another array of floats which -again in groups of 3- describe vertices of the catmull rom spline.

On each of these vertices, I want to create a ring of vertices which also can differ in density (amount of smoothness / vertices per ring).

All former vertices (control points and those that describe the catmull rom spline) are discarded.

Only the vertices that form the tube rings will be passed to OpenGL, which in turn will connect those to form the final tube.

I am as far as being able to create the catmullrom spline, and create rings at the position of its vertices, however, they are all on a planars that are in the same angle, instead of following the splines path.

[/edit]

Thanks!

Answer 1

Suppose you have a parametric curve such as:

xx[t_] := Sin[t];
yy[t_] := Cos[t];
zz[t_] := t;  

Which gives:

The tangent vector to our curve is formed by the derivatives in each direction. In our case

Tg[t_]:= {Cos[t], -Sin[t], 1}  

The orthogonal plane to that vector comes solving the implicit equation:

Tg[t].{x - xx[t], y - yy[t], z - zz[t]} == 0  

In our case this is:

-t + z + Cos[t] (x - Sin[t]) - (y - Cos[t]) Sin[t] == 0  

Now we find a circle in that plane, centered at the curve. i.e:

c[{x_, y_, z_, t_}] := (x - xx[t])^2 + (y - yy[t])^2 + (z - zz[t])^2 == r^2  

Solving both equations, you get the equation for the circles:

HTH!

Edit

And by drawing a lot of circles, you may get a (not efficient) tube:

Or with a good Graphics 3D library:

Edit

Since you insist :) here is a program to calculate the circle at junctions.

a = {1, 2, 3}; b = {3, 2, 1}; c = {2, 3, 4};
l1 = Line[{a, b}];
l2 = Line[{b, c}];

k = Cross[(b - a), (c - b)] + b; (*Cross Product*)
angle = -ArcCos[(a - b).(c - b)/(Norm[(a - b)] Norm[(c - b)])]/2;
q = RotationMatrix[angle, k - b].(a - b);
circle[t_] := (k - b)/Norm[k - b] Sin@t + (q)/Norm[q] Cos@t + b;

Show[{Graphics3D[{
    Red, l1,
    Blue, l2,
    Black, Line[{b, k}],
    Green, Line[{b, q + b}]}, Axes -> True],
  ParametricPlot3D[circle[t], {t, 0, 2 Pi}]}]

Edit

Here you have the mesh constructed by this method. It is not pretty, IMHO:

Answer 2

You need to look at Fenet formulas in Differential Geometry. See figure 2.1 for an example with a helix.

Surfaces & Curves

Answer 3

I don't know what your language of choice is, but if you speak MatLab there are already a few implementations available. Even if you are using another language, some of the code might be clear enough to inspire a reimplementation.

The key point is that if you don't want your tube to twist when you connect the vertices, you cannot determine the basis locally, but need to propagate it along the curve. The Frenet frame, as proposed by jalexiou, is one option but simpler stuff works fine as well.

I did a simple MatLab implementation called tubeplot.m in my formative years (based on a simple non-Frenet propagation), and googling it, I can see that Anders Sandberg from kth.se has done a (re?)implementation with the same name, available at http://www.nada.kth.se/~asa/Ray/Tubeplot/tubeplot.html.

Edit: The following is pseudocode for the simple implementation in tubeplot.m. I have found it to be quite robust.

The plan is to propagate two normals a and b along the curve, so that at each point on the curve a, b and the tangent to the curve will form an orthogonal basis which is "as close as possible" to the basis used in the previous point. Using this basis we can find points on the circumference of the tube.

// *** Input/output ***
// v[0]..v[N-1]: Points on your curve as vectors
//               No neighbours should overlap
// nvert: Number of vertices around tube, integer.
// rtube: Radius of tube, float.
// xyz: (N, nvert)-array with vertices of the tube as vectors


// *** Initialization ***
// 1: Tangent vectors
for i=1 to N-2:
    dv[i]=v[i+1]-v[i-1]
dv[0]=v[1]-v[0], dv[N-1]=v[N-1]-v[N-2]

// 2: An initial value for a (must not be pararllel to dv[0]):
idx=<index of smallest component of abs(dv[0])>
a=[0,0,0], a[idx]=1.0

// *** Loop ***
for i = 0 to N-1:
    b=normalize(cross(a,dv[i]));
    a=normalize(cross(dv[i],b));
    for j = 0 to nvert-1:
        th=j*2*pi/nvert 
        xyz[i,j]=v[i] + cos(th)*rtube*a + sin(th)*rtube*b

Implementation details: You can probably speed up things by precalculating the cos and sin. Also, to get a robust performance, you should fuse input points closer than, say, 0.1*rtube, or a least test that all the dv vectors are non-zero.

HTH

Answer 4

Taking the cross product of the line segment and the up vector will give you a vector at right-angles to them both (unless the line segment points exactly up or down) which I'll call horizontal. Taking the cross product of horizontal and the line segment with give you another vector that's at right angles to the line segment and the other one (let's call it vertical). You can then get the circle coords by lineStart + cos theta * horizontal + sin theta * vertical for theta in 0 - 2Pi.

Edit: To get the points for the mid-point between two segments, use the sum of the two line segment vectors to find the average.