Fastest method to solve multiple nonlinear independent equations in MATLAB?

Question

MATLAB has two methods to solve a nonlinear equation:

• fzero: solves a single nonlinear equation
• fsolve: solves a system of nonlinear equations

Therefore, one can use the following methods to solve a system of n nonlinear independent equations:

1. Use a loop to solve the equations separately using fzero
2. Use a loop to solve the equations separately using fsolve
3. Use fsolve to solve them together

My intuition would be that:

• A loop method is faster than a single system for large n as complexity (gradient calculation) is 0(n^2)
• A loop may be slower for small n as a loop has a high overhead in MATLAB and there may be some constant startup time
• fzero is faster than fsolve as it is specifically made for a single nonlinear equation.

Question: What is the fastest method to a system of n nonlinear independent equations? Are there other methods? Which options should be used to speed up the process?

Example problem: (may be used to benchmark different answers)

x_i^2 = 1

with i between 1 and n

Related threads

• Solving multiple independent non linear equations
• Solve a large number of independent nonlinear equations with fsolve without loops

Answer 1

The best approach to evaluate the performance of some method is to write a benchmark. Four cases are considered:

1. loop fzero: uses a loop to solve the equations separately using fzero
2. loop fsolve: uses a loop to solve the equations separately using fsolve
3. default fsolve: solves the equations together as one system of equations
4. independent fsolve: same as default fsolve, but specifies that the equations are independent

---

f = @(x) x.^2-1; % the set of non-linear equations
ns = 1:1:100; % the sizes for which the benchmark is performed
options=optimset('Display','off'); % disable displaying

figure
hold on
plot(ns, loopFSolve(f, ns, options), 'DisplayName', 'loop fsolve')
plot(ns, loopFZero(f, ns, options), 'DisplayName', 'loop fzero')
plot(ns, defaultFSsolve(f, ns, options), 'DisplayName', 'default fsolve')
plot(ns, independentFSolve(f, ns, options), 'DisplayName', 'independent fsolve')

legend ('Location', 'northwest')

function t = loopFZero(f, ns, options)
  t1 = timeit(@() fzero(f, rand(1), options));
  t = ns * t1;
end

function t = loopFSolve(f, ns, options)
  t1 = timeit(@() fsolve(f, rand(1), options));
  t = ns * t1;
end

function t = defaultFSsolve(f, ns, options)
  t = zeros(size(ns));
  for i=1:length(ns)
    n = ns(i);
    un = rand(n, 1);
    t(i) = timeit(@() fsolve(f, un, options));
  end
end

function t = independentFSolve(f, ns, options)
  t = zeros(size(ns));
  for i=1:length(ns)
    n = ns(i);
    un = rand(n, 1);
    options.Algorithm = 'trust-region-reflective';
    options.JacobPattern = speye(n);
    options.PrecondBandWidth = 0;

    t(i) = timeit(@() fsolve(f, un, options));
  end
end

Results

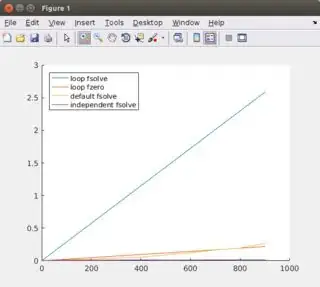
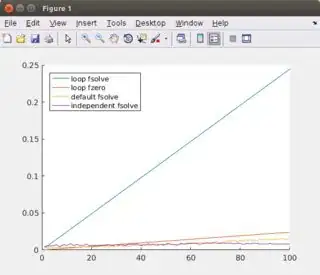
All the figures show the computation time for the complete system in function of n, the number of equations.

The first two figures plot n up to 1000, with an interval of 100. The last two figures plot n up to 100 with an interval of 1. For each, the second plot is the same as the first one but without loop fzero as it is much slower than the others.

Conclusion

1. loop fsolve: do not use it, startup time is too high
2. loop fzero: you can use it for small n (fastest method for n < ~20)
3. default fsolve: you can use it for relative small n (fastest method for ~20 < n < ~50, but difference with 2 and 3 is relative small).
4. independent fsolve: you should use it for large n (fastest method for ~50 < n)

In general, you should use independent fsolve, only for small n loop fzero may be used instead, i.e. use fsolve with the following options:

options.Algorithm = 'trust-region-reflective';
options.JacobPattern = speye(n);
options.PrecondBandWidth = 0;

Lazy people may just use the default fsolve as it has a reasonable performance for a moderate number of equations (n < ~200)

Important remark

Bob pointed out that a vectorised version of fzero may be multiple orders of magnitude faster. According to Bob's test results, his method is the fastest method for every size of the problem, i.e. large and small n.

Remarks

• Note that the time complexity of default fsolve is O(n^2) while the others are O(n).
• Note that fzero and fsolve may behave differently in some boundary cases, f.e fzero will not found a solution for x^2 as it searches the location of a sign change.

Answer 2

I'm adding this answer to elaborate on my comment above. In my experience by far the fastest method is to use a vectorized version of fzero that is available on the file exchange: Link to vectorized bisection code

Here is a couple of benchmarks comparing it's performance to (i) looped fzero and (ii) independent fsolve.

f = @(x) x.^2-1; %the set of non-linear equations
ns = 1e5; %size of the problem

% method 1: looped fzero
t = timeit(@() fzero(f, rand(1)));
loopFZero = t*ns

% method 2: independent fsolve
options=optimset('Display','off'); % disable displaying
options.Algorithm = 'trust-region-reflective';
options.JacobPattern = speye(ns);
options.PrecondBandWidth = 0;
indepFSolve = timeit(@() fsolve(f, rand(ns,1), options))

% method 3: vectorized bisection, available here:
% https://www.mathworks.com/matlabcentral/fileexchange/28150-bisection-method-root-finding
vecBisection = timeit(@() bisection(f, zeros(ns,1), 2))

Results

%---------------
% ns = 10

loopFZero =

    0.0027


indepFSolve =

    0.0049


vecBisection =

   5.0978e-05

%---------------
% ns = 1e5

loopFZero =

   28.7574


indepFSolve =

    7.7601


vecBisection =

    0.0013