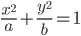How to find the equation for an ellipse

Question

I am looking to find the equation for an ellipse given five or six points using the general equation for a conic: A x2 + B xy + C y2 + D x + E y + F = 0.

At first I tried using six points. Here is my python code:

    import numpy as np
    def conic_section(p1, p2, p3, p4, p5, p6):
        def row(point):
            return [point[0]*point[0], point[0]*point[1], point[1]*point[1],                         
            point[0], point[1], 1]
        matrix=np.matrix([row(p1),row(p2),row(p3),row(p4),row(p5), row(p6)])
        b=[0,0,0,0,0,0]
        return np.linalg.solve(matrix,b)

    print conic_section(np.array([6,5]), np.array([2,9]), np.array([0,0]),         
    np.array([11, 5.5]), np.array([6, 7]), np.array([-1,-1]))

The problem is that this will return the solution [0,0,0,0,0,0] because the right hand side of my equation is the zero vector.

I then attempted to change the conic by subtracting the F and dividing it through:

A x2 + B xy + C y2 + D x + E y + F = 0

A x2 + B xy + C y2 + D x + E y = -F

A' x2 + B xy + C' y2 + D' x + E' y = -1.

The reason that this doesn't work though is that if one of my point is (0,0), then I would end up with a Matrix that has a row of zeros, yet the right hand side of the equation would have a -1 for the entries in the vector. In other words, if one of my points is (0,0) - then "F" should be 0, and so I can't divide it out.

Any help would be appreciated. Thank You.

What do you mean you can't divide it out? Linear algebra is perfectly capable to handle this. Given the six point are *independent*, and are on the ellipse, the system can solve the equation. — Willem Van Onsem, Jun 24 '17 at 21:55
If a ellipse has any point touching the origin, the F value in its equation is equal to 0. :) In that case I don't think you can use this method if you have an ellipse without a constant. Someone correct me if I'm wrong. — cs95, Jun 24 '17 at 22:03
If F=0 then you can't divide the equation by F, because you can't divide by zero. Five points which don't work are simply the first five listed: np.array([6,5]), np.array([2,9]), np.array([0,0]), np.array([11, 5.5]), np.array([6, 7]). — Jbag1212, Jun 24 '17 at 22:32
If you know you've got an ellipse (rather than a more general conic section), `A` must be nonzero. Since you can scale `A` through `F` by an arbitrary factory, you could add an extra constraint `A = 1` to your set of linear equations (and if you have six points, then drop one of them; five are enough to determine the conic). — Mark Dickinson, Jun 25 '17 at 17:36

score 4 · Accepted Answer · answered Jun 25 '17 at 02:41

It seems that you have exact points on ellipse, don't need approximation, and use Braikenridge-Maclaurin construction for conic sections by some strange way.

Five points(x[i],y[i]) determines ellipse with this explicit equation (mathworld page, eq. 8)

So to find ellipse equation, you can build cofactor expansion of the determinant by minors for the first row. For example, coefficient Ais determinant value for submatrix from x1y1 to the right bottom corner, coefficient B is negated value of determinant for submatrix without xiyi column and so on.

glegoux · Answer 2 · 2017-06-25T17:46:46.737

Ellipse equation (without translation and rotation):

$\frac{x^2}{a} + \frac{y^2}{b} = 1$

The goal is to resolve this linear equation in variable A through F:

Ax^2 + Bxy + Cy^2 + Dx + Ey + F = 0

Use:

from math import sin, cos, pi, sqrt

import matplotlib.pyplot as plt
import numpy as np
from numpy.linalg import eig, inv

# basis parameters of the ellipse
a = 7
b = 4

def ellipse(t, a, b):
    return a*cos(t), b*sin(t)

points = [ellipse(t, a, b) for t in np.linspace(0, 2*pi, 100)]
x, y = [np.array(v) for v in list(zip(*points))]

fig = plt.figure()
plt.scatter(x, y)
plt.show()

def fit_ellipse(x, y):
    x = x[:, np.newaxis]
    y = y[:, np.newaxis]
    D =  np.column_stack((x**2, x*y, y**2, x, y, np.ones_like(x)))
    S = np.dot(D.T, D)
    C = np.zeros([6,6])
    C[0, 2] = C[2, 0] = 2
    C[1, 1] = -1
    E, V = eig(np.dot(inv(S), C))
    n = np.argmax(np.abs(E))
    return V[:, n]

A, B, C, D, E, F = fit_ellipse(x, y)
K = D**2/(4*A) + E**2/(4*C) - F

# a, b
print('a:', sqrt(K/A), 'b:', sqrt(K/C))

Output:

a: 6.999999999999998 b: 4.0

See:

http://mathworld.wolfram.com/ConicSection.html https://fr.wikipedia.org/wiki/Ellipse_(math%C3%A9matiques)#Forme_matricielle http://nicky.vanforeest.com/misc/fitEllipse/fitEllipse.html

The equations _are_ linear in the unknowns, which are `A` through `F`. The OPs problem is coming from that fact that these are _homogeneous_ linear equations. — Mark Dickinson, Jun 25 '17 at 17:28

How to find the equation for an ellipse

2 Answers2