Cost Optimization for different suppliers depending on quantities

Question

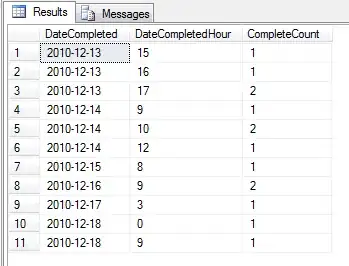
I am trying to optmize the minimum cost based on suppliers' cost for one product.

The first restriction is that the price varies based on cost, so on the 1st supplier, if you buy 1<=x<5 the price is 107 and if x>=5 the price is 90.

Another restriction is that if the cost is the same BodeBrown>Bil Bil> Homebrewer (I have no idea how to implement it, maybe sum an insignificant number to the cost ordenated)

And there is a demand for each production period.

I tried to use binaries to exclude one price of each supplier, making an OR logic. eg.: x1+x2<=1. And make an Objective Function like minimize z: 107*x1+90*x2+100*x3+96*x4+105*x5+90*x6 with var xi>=0, binary;

However, i couldn't implement the demand with the binary.

If someone could give me some tip, please. Thanks in advance

ps.:I am learning LP on Gusek, but i also installed solverstudio

Edit2:

I came with this solution:

It was solved on LINGO, thanks to Erwin!

@BIN( y1);
@BIN( y2);
@BIN( y3);
@BIN( y4);
@BIN( y5);
@BIN( y6);
@GIN( x1);
@GIN( x2);
@GIN( x3);
@GIN( x4);
@GIN( x5);
@GIN( x6);
!Desempate;
e1=0.001;
e2=0.001;
e3=0.002;
e4=0.002;
e5=0.003;
e6=0.003;
!FO;
!Sum(ci*xi*yi);
MIN = ((107+e1)*x1*y1)+((90+e2)*x2*y2)+((100+e3)*x3*y4)+((96+e4)*x4*y4)+((105+e5)*x5*y5)+((90+e6)*x6*y6);

!s.t.;
!Demand, it is a variable that is changed during production;
x1*y1+x2*y2+x3*y3+x4*y4+x5*y5+x6*y6=5;
!Just one supplier is chosen;
y1+y2+y3+y4+y5+y6=1;
!Intervals;
x1>=1*y1;
x1<5*y1;
x2>=5*y2;
x3>=1*y3;
x3<4*y3;
x4>=4*y4;
x5>=1*y5;
x5>5*y5;
x6>=5*y6;

Well, the program is messy, but it is just for learning, with the formulas It is possible to make a general programming and solve larger problems.

This is often modeled using piecewise linear functions. This can be done with SOS2 variables or binary variables. — Erwin Kalvelagen, Jun 23 '17 at 05:26
And Thank you for the tips, i am looking into Piecewise linear function, it is what i needed to make it work — danieltakeshi, Jun 23 '17 at 11:45
Thank you! I had an idea and am editing the post, is it correct? — danieltakeshi, Jun 23 '17 at 17:21
Does Gusek solve this kind of problem with accuracy? or do i have to rewrite it to LP? It is the only way i came with to solve this problem — danieltakeshi, Jun 23 '17 at 19:47
Gusek is not a solver, just an editor. GLPK does not allow nonlinear objectives (or nonlinear anything). believe GLPK also does not support SOS2 variables. It is possible to simulate SOS2 sets with binary variables. See H.P. Williams, "Model Building in Mathematical Programming", Wiley, — Erwin Kalvelagen, Jun 23 '17 at 20:40
Thank you, i suceeded to solve it on Lingo Demo, going to implement on SolverStudio or OpenSolver — danieltakeshi, Jun 24 '17 at 01:26
Note again that there are better and linear formulations for this problem. Your formulation is non-linear. — Erwin Kalvelagen, Jun 25 '17 at 21:45
Yeah, i saw some methods to transform non-linear into linear. However, since it solver my problem it is ok. I am not used to program on this language, so i use my experience on other languages to try to formulate the problem and it ends on flawed formulations — danieltakeshi, Jun 26 '17 at 11:56

Cost Optimization for different suppliers depending on quantities

0 Answers0