4

I am trying to better understand aspects/implications of the observed versus expected information in the context of maximum likelihood estimation. Part of this involves simulating data. If I generate outcome data from the following logistic model:

set.seed(123)
n <- 5000
c1 <- rnorm(n,3,1.5)
c2 <- rnorm(n,5,1.75)
x <- rnorm(n,1+1.25*c1+1.75*c2,1.5)
p<-1/(1+exp(-(-13.5+log(1.5)*x+log(1.25)*c2+log(1.75)*c2)))
y <- rbinom(n,1,p)
dat<-data.frame(c1,c2,x,y)

Then then, if I understood correctly, this code gives me the observed information matrix:

a<-glm(y~x+c1+c2,data=dat,family=binomial(link="logit"))
solve(vcov(a))

But I can't figure out how to obtain the expected information matrix.

Ashley Naimi
  • 232
  • 1
  • 9

1 Answers1

2

But I can't figure out how to obtain the expected information matrix.

Firstly, the observed information matrix and the expected information matrix coincide in this case since you use a canonical link function (see this wiki page and the reference).

..., if I understood correctly, this code gives me the observed information matrix

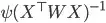Secondly, vcov gives you formula (see getS3method("vcov", "glm") and getS3method("summary", "glm")) where psi is the dispersion parameter, X is the design matrix and W is the working weighs. AFAIR the IWLS method used by glm is equivalent to Fischer scoring also when a non-canonical link function is used. Consequently, this would be the expected information matrix and not the observed information matrix.

Benjamin Christoffersen
  • 4,703
  • 15
  • 37