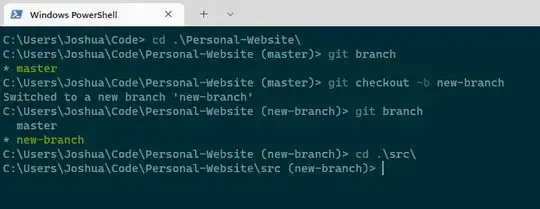
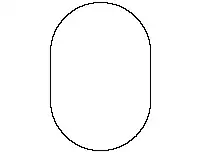
How can I draw outline of thick line such as one below in vector form? By vector form I mean some collection of Graphics primitives that's not Raster or Image.
Graphics[{AbsoluteThickness[100], JoinForm["Round"], CapForm["Round"],
Line[{{0, 0}, {0, 1}, {1, 1}}]}, ImageSize -> 200]

(source: yaroslavvb.com)
Documentation has the following example for extracting outlines of text, but I haven't found a way to modify it to get outlines of Line objects
ImportString[ExportString[Style["M8", FontFamily -> "Times", FontSize -> 72],"PDF"], "TextMode" -> "Outlines"]
I've also tried doing Rasterize on the line object and subtracting a slightly smaller version from the alpha channel. That gives rasterization artifacts, and is too slow at 5 seconds per shape for ImageSize->500
also asked on mathgroup
Update
I've tried fitting spline through points you get from MorphologicalPerimeter. ListCurvePathPlot theoretically does it, but it breaks on pixel "staircase" pattern. To smooth the staircase one needs to find ordering of points around the curve. FindCurvePath seemed promising, but returned list of broken curves. FindShortestTour could also theoretically do this, but it took over a second on outline in a 20x20 pixel image. ConvexHull does perfect job on round parts, but cuts off the non-convex part.
Solution I finally ended up with was constructing nearest neighbor graph over perimeter points and using version 8 function FindEulerianCycle to find the ordering of pixels around the shape, then using MovingAverage to smooth out the staircase, followed by ListCurvePathPlot to create the spline object. It's not perfect, as there's still a remnant of "staircase" pattern whereas averaging too much will smooth out important corners. A better approach might break the shape into multiple convex shapes, use ConvexHull, then recombine. Meanwhile, here's what I'm using
getSplineOutline[pp_, smoothLen_: 2, interOrder_: 3] := (
(* need to negate before finding perimeter to avoid border *)
perim = MorphologicalPerimeter@ColorNegate@pp;
points =
Cases[ArrayRules@SparseArray@ImageData[perim],
HoldPattern[{a_Integer, b_Integer} -> _] :> {a, b}];
(* raster coordinate system is upside down, flip the points *)
points = {1, -1} (# - {0, m}) & /@ points;
(* make nearest neighbor graph *)
makeEdges[point_] := {Sort[{point, #}]} & /@
Nearest[DeleteCases[points, point], point];
edges = Union[Flatten[makeEdges /@ points, 2]];
graph = Graph[UndirectedEdge @@@ edges];
tour = FindEulerianCycle[graph] // First;
smoothed = MovingAverage[tour[[All, 1]], smoothLen];
g = ListCurvePathPlot[smoothed, InterpolationOrder -> interOrder];
Cases[g, BSplineCurve[___], Infinity] // First
);
scale = 200;
pp = Graphics[{AbsoluteThickness[scale/2], JoinForm["Round"],
CapForm["Round"], Line[{{0, 0}, {0, 1}, {1, 1}}]},
ImageSize -> scale];
Graphics[getSplineOutline[pp, 3, 3]]

(source: yaroslavvb.com)