12

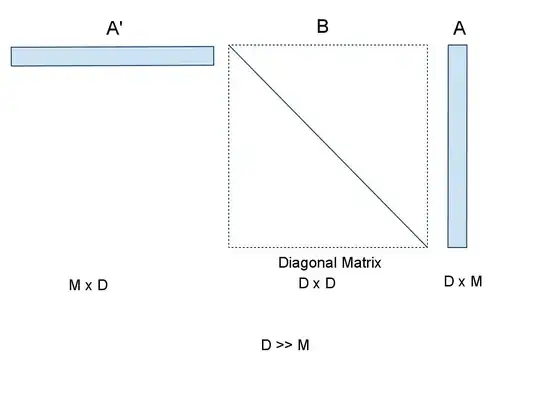
I don't have enough memory to simply create a diagonal D-by-D matrix, since D is large. I keep getting an 'out of memory' error.

Instead of performing M x D x D operations in the first multiplication, I do M x D operations, but still my code takes ages to run.

Can anybody find a more effective way to perform the multiplication A'*B*A? Here's what I've attempted so far:

D=20000
M=25

A = floor(rand(D,M)*10);
B = floor(rand(1,D)*10);

for i=1:D
    for j=1:M
        result(i,j) = A(i,j) * B(1,j);
    end
end    

manual = result * A';
auto = A*diag(B)*A';
isequal(manual,auto)

alt text

matcheek
  • 4,887
  • 9
  • 42
  • 73

3 Answers3

12

One option that should solve your problem is using sparse matrices. Here's an example:

D = 20000;
M = 25;
A = floor(rand(D,M).*10);    %# A D-by-M matrix
diagB = rand(1,D).*10;       %# Main diagonal of B
B = sparse(1:D,1:D,diagB);   %# A sparse D-by-D diagonal matrix
result = (A.'*B)*A;         %'# An M-by-M result

Another option would be to replicate the D elements along the main diagonal of B to create an M-by-D matrix using the function REPMAT, then use element-wise multiplication with A.':

B = repmat(diagB,M,1);   %# Replicate diagB to create an M-by-D matrix
result = (A.'.*B)*A;    %'# An M-by-M result

And yet another option would be to use the function BSXFUN:

result = bsxfun(@times,A.',diagB)*A;  %'# An M-by-M result
gnovice
  • 125,304
  • 15
  • 256
  • 359
  • 2
    if memory is an issue, the `bsxfun` is preferred to `repmat`, because it does not spawn a replicated matrix. However, `bsxfun` did not become available until Matlab 2006 or so... – shabbychef Dec 12 '10 at 06:59
3

Maybe I'm having a bit of a brainfart here, but can't you turn your DxD matrix into a DxM matrix (with M copies of the vector you're given) and then .* the last two matrices rather than multiply them (and then, of course, normally multiply the first with the found product quantity)?

Yonatan N
  • 306
  • 1
  • 11
  • I'm not creating D x D because of 'out of memory error' it'd be easy then. Your solution gives me an 'out of memory' error almost on the spot mine takes a bit longer but does exactly the same. They are both correct,but the matrices are huge. – matcheek Dec 12 '10 at 04:50
  • Both my solution and gnovice only require O(DxM) storage. I don't see why my solution is incorrect whereas his is fine. In fact, his repmat solution is mine exactly (up to order of multiplication, which doesn't matter). – Yonatan N Dec 12 '10 at 06:52
  • thank you for your answer. To make it clear, I did try your solution but could not overcome the 'out of memory' error. – matcheek Dec 12 '10 at 07:09
3

  1. You are getting "out of memory" because MATLAB can not find a chunk of memory large enough to accommodate the entire matrix. There are different techniques to avoid this error described in MATLAB documentation.

  2. In MATLAB you obviously do not need programming explicit loops in most cases because you can use operator *. There exists a technique how to speed up matrix multiplication if it is done with explicit loops, here is an example in C#. It has a good idea how (potentially large) matrix can be split into smaller matrices. To contain these smaller matrices in MATLAB you can use cell matrix. It is much more probably that system finds enough RAM to accommodate two smaller sub-matrices then the resulting large matrix.

Doubt
  • 1,163
  • 2
  • 15
  • 26
Mikhail Poda
  • 5,742
  • 3
  • 39
  • 52
  • 1
    I'm a big ignoramus and haven't event thought for a moment about cache misses, loop unrolling or branch prediction, but thanks for a reminder – matcheek Dec 12 '10 at 08:29
  • @matcheek: the technique of splitting a large matrix into smaller ones can be applied to the RAM the same way it is applied to the cache. For you cache does not matter at all, but RAM does. – Mikhail Poda Dec 12 '10 at 08:39