How to determine which language is simpler

Question

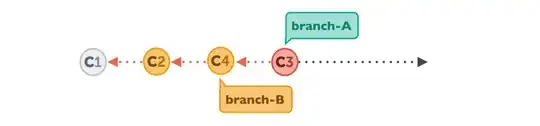
The following language is the complement of a simpler language. Construct a DFA for the simpler language and then use it to give the state diagram of a DFA for the given language where Σ = {a,b}.

L={ w : w does not contain the substring baba}.

I don't know which is the simpler language, can anybody please explain?

score 0 · Answer 1 · answered May 18 '17 at 21:16

0

It's been a while since my Logic & Computability class, but my guess is the complement language Lc would be = { w: w contains the substring 'baba'}.

It's probably pretty easy to make a DFA that accepts substrings of 'baba', you'd probably just have states firstB, firstA, secondB, and secondA and so on.

Making a complement DFA then is trivial, just make the accepting states non-accepting and vice versa.

answered May 18 '17 at 21:16

brupbrap

1
4

so is what was meant by "simpler language" is { w: w contains the substring 'baba'}. from which i will turn the ccepting states into non-accepting and vice versa as u mentioned?? – nmorsi May 18 '17 at 22:10

score 0 · Accepted Answer · edited Jun 20 '20 at 09:12

0

The automata accepting any word containing the substring 'baba' is:

(it's the simpler language. A regexp for it is : (a|b)*baba(a|b)* )

And we can build the complement DFA by turning accepting states into non-accepting and vice-versa as you mentionned it:

(it has to completed)

edited Jun 20 '20 at 09:12

Community

1
1

answered May 19 '17 at 10:42

Gerard Rozsavolgyi

4,834
4
32
39

thanks alot.. state 5 is omitted because its a dead state or unreachable one, right?? – nmorsi May 19 '17 at 11:27
yes, it's a dead state. you can add it to get a complete DFA – Gerard Rozsavolgyi May 19 '17 at 11:32

How to determine which language is simpler

2 Answers2