Confusion regarding the quick union algorithm when applied to the sequence of pairs: 1-2,2-3,3-4

Question

As far as my understanding goes in the quick-union algorithm when a pair is to be processed we first do the FIND operation and check if the roots of the trees in which these objects are present are equal or not. In the case they are not equal we perform the UNION operation by linking the 2 different roots.

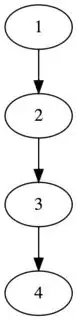
In Sedgewick pg-15 property:1.2-"Suppose that the input pairs come in the order 1-2, then 2-3, then 3-4 and so forth. After N-1 such pairs, we have N objects all in the same set, and the tree that is formed by the quick-union algorithm is a straight line, with N pointing to N-1, which points to N - 2,which points to N - 3, and so forth."

According to me the tree formed has the root 1 and all other objects from 2 to N are its children-when we scan 1-2,there roots are themselves so we link them,when we scan 2-3,the root of 2 is 1 the root of 3 is 3 itself so we link 1 and 3 and not 2 and 3.

How can the tree be a straight line in this instance?

#include <stdio.h> 

#define N 10000 

main() 

{   int i, p, q, t, id[NJ; 

for (i = 0; i < N; i++) id[i] = i; 

while (scanfC"%d %d\n", &p, &q)==2)
{

for(i=p;i!=id[i];i=id[i]);

for(j=q;j!=id[j];j=id[j]);

if(i==j) continue;

id[i]=j;

printf("%d%d\n",p,q);

}
}

@Henry Could i send you a screenshot of the relevant material? — iosdev, May 06 '17 at 06:13
I don't see any implementation here, just a description of a general algorithm. — Antti Haapala -- Слава Україні, May 06 '17 at 06:31
@AnttiHaapala yes, they aren't here, the book is algorithms in C, so i thought a C coder cluld offer some clarification. — iosdev, May 06 '17 at 06:33
It's hard to answer this question without the specific details of the quick-union implementation that Sedgwick is describing. — Paul Hankin, May 06 '17 at 07:35
@PaulHankin I have added the program now,we can get a straight line as per the situation described by the answer below but what of the direction of the pointers? — iosdev, May 06 '17 at 09:52

score 0 · Answer 1 · answered May 06 '17 at 06:16

0

There is a case where you can form a straight line:

1-2  leads to 1->2
2-3  the root of 2 is 2 and the root of 3 is 3 so link 2 to 3: 1->2->3
3-4  the roots are 3 and 4 so link 3 to 4: 1->2->3->4
...

However the links would go in the opposite direction as described.

answered May 06 '17 at 06:16

Henry

42,982
7
68
84

But as per the algorithm we have to find the roots of the 2 trees and link the roots, after 1-->2,the root of 2 becomes 1,so when processing 2-3, we cannot say that the root of 2 is 2 itself, it has become 1 now, so we should link it with 1. – iosdev May 06 '17 at 06:20
but you can link the two roots either as 1->2 or as 2->1; I have chosen the first here. So the root of 2 is 2 (and 2 is also the root of 1). – Henry May 06 '17 at 06:22
Thank you, i understand it now. – iosdev May 06 '17 at 06:27

Paul Hankin · Answer 2 · 2017-05-06T10:35:32.580

Finding some way to visualize the union find structure produced will probably help you. Using a cleaned up version of your code that uses the static data provided by Sedgwick, and generates a dot file of the final structure for visualization, one gets this dot file (with arrows meaning x->id[x]).

digraph unionfind {
    "1" -> "2"
    "2" -> "3"
    "3" -> "4"
}

Which renders as this graph, using http://dreampuf.github.io/GraphvizOnline/

Here's the cleaned up code with dot file generation. You can play around with changing the data array to see the effects of different orders or unions. The visualized graph doesn't include nodes in the structure that are neither the parent or child of another node.

#include <stdio.h>

#define N 10000

int data[][2] = {
    {1, 2},
    {2, 3},
    {3, 4}
};

int main() {
    int id[N];
    for (int i=0; i<N; i++) id[i] = i;

    for (int di=0; di<sizeof(data)/sizeof(data[0]); di++) {
        int p = data[di][0];
        int q = data[di][1];

        int i, j;
        for(i=p; i!=id[i]; i=id[i]);
        for(j=q; j!=id[j]; j=id[j]);
        if(i==j) continue;
        id[i]=j;
    }
    printf("digraph unionfind {\n");
    for (int i=0; i<N; i++) {
        if (id[i] == i) continue;
        printf("    \"%d\" -> \"%d\"\n", i, id[i]);
    }
    printf("}\n");
    return 0;
}

Confusion regarding the quick union algorithm when applied to the sequence of pairs: 1-2,2-3,3-4

2 Answers2