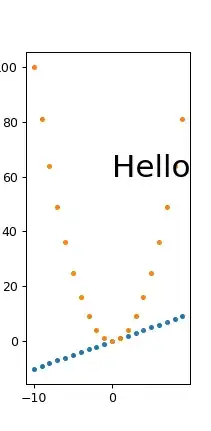
Im trying to arrange line segments to create a closed polygon with python. At the moment I've managed to solve it but is really slow when the number of segments increase (its like a bubble sort but for the end point of segments). I'm attaching a sample file of coordinates (the real ones are really complex but is useful for testing purposes). The file contains the coordinates for the segments of two separetes closed polygons. The image below is the result of the coordinates I've attached.
 This is my code for joining the segments. The file 'Curve' is in the dropbox link above:
This is my code for joining the segments. The file 'Curve' is in the dropbox link above:
from ast import literal_eval as make_tuple
from random import shuffle
from Curve import Point, Curve, Segment
def loadFile():
print 'Loading File'
file = open('myFiles/coordinates.txt','r')
for line in file:
pairs.append(make_tuple(line))
file.close()
def sortSegment(segPairs):
polygons = []
segments = segPairs
while (len(segments) > 0):
counter = 0
closedCurve = Curve(Point(segments[0][0][0], segments[0][0][1]), Point(segments[0][1][0], segments[0][1][1]))
segments.remove(segments[0])
still = True
while (still):
startpnt = Point(segments[counter][0][0], segments[counter][0][1])
endpnt = Point(segments[counter][1][0], segments[counter][1][1])
seg = Segment(startpnt, endpnt)
val= closedCurve.isAppendable(seg)
if(closedCurve.isAppendable(seg)):
if(closedCurve.isClosed(seg)):
still =False
polygons.append(closedCurve.vertex)
segments.remove(segments[counter])
else:
closedCurve.appendSegment(Segment(Point(segments[counter][0][0], segments[counter][0][1]), Point(segments[counter][1][0], segments[counter][1][1])))
segments.remove(segments[counter])
counter = 0
else:
counter+=1
if(len(segments)<=counter):
counter = 0
return polygons
def toTupleList(list):
curveList = []
for curve in list:
pointList = []
for point in curve:
pointList.append((point.x,point.y))
curveList.append(pointList)
return curveList
def convertPolyToPath(polyList):
path = []
for curves in polyList:
curves.insert(1, 'L')
curves.insert(0, 'M')
curves.append('z')
path = path + curves
return path
if __name__ == '__main__':
pairs =[]
loadFile();
polygons = sortSegment(pairs)
polygons = toTupleList(polygons)
polygons = convertPolyToPath(polygons)