2

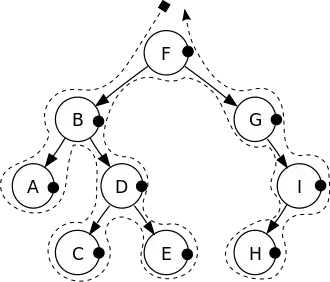
Let I have some expression as 2*3/(2-1) +5*(4-1) . It is infix notation. Of course I can construct for this expression a tree that you can see on image. enter image description here

Then, let's write this expression in postfix and prefix forms. Postfix: 2 3 * 2 1 - / 5 4 1 - * + Prefix : + / * 2 3 - 2 1 * 5 - 4 1

And the question is: a tree for above expressions will be the same? If not,how to construct it?

neo
  • 1,314
  • 2
  • 14
  • 34

3 Answers3

3

And the question is: a tree for above expressions will be the same?

Yes, it's the same tree -- the different notations represent the same calculation.

The different ways to write the expression correspond just to different traversals of the same tree:

  • pre-order for prefix notation

enter image description here

(pre-order: F, B, A, D, C, E, G, I, H)

  • in-order for infix notation

enter image description here

(in-order: A, B, C, D, E, F, G, H, I)

  • post-order for postfix notation

enter image description here

(post-order: A, C, E, D, B, H, I, G, F)

danbanica
  • 3,018
  • 9
  • 22
3

Here's a rough sketch of constructing the tree from the prefix representation (think of the prefix notation as a stream of numbers and operators):

preocedure buildTree(prefix):
    c := first item of prefix
    if c is a number then
        return a tree node containing the number
    else
        create a tree node t with c (an operator in this case)
        t.left := buildTree(rest of prefix)
        t.right := buildTree(rest of prefix)
        return t

You should call this method with the prefix representation of the tree. The method will recursively build the subtrees from it.

You can also write a similar method to build the tree from the postfix representation also. You'll need to tweak this algorithm to start from the right end and build the right subtree first.

Sufian Latif
  • 13,086
  • 3
  • 33
  • 70
3

There are plenty of resources out there on how to construct a expression tree. wiki here has a very good reference.

The idea is that as you iterate through each character, for example, the postfix expression.

  • If the character is a operand then you push it onto the stack

  • If the character is a operator, then you pop two elements from the stack and make them the childen of the current operator, then you push the operator to the stack.

After the loop terminates, you would end up with a single element on the stack as the root to the tree.

夢のの夢
  • 5,054
  • 7
  • 33
  • 63