-1

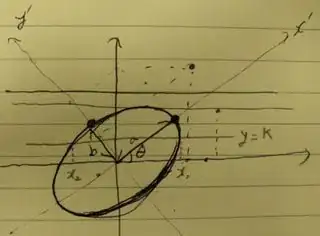
Tilted ellipse

As the above link figure shows, let's assume that we have a tilted ellipse, say "theta" angle from its original position. How can we get the coordinate of x1, x2 which have a same y value? Either getting it analytically, or numerically would be okay. But maybe numerical approaches using, for example, Python would be more appropriate for this community and promising, I guess.

tripleee
  • 175,061
  • 34
  • 275
  • 318
Jinho Ryu
  • 1
  • Can you show the code you attempted to solve the problem? – thewaywewere Apr 20 '17 at 15:32
  • Welcome to Stack Overflow. Check the Stack Overflow's [help on asking questions](http://stackoverflow.com/help/asking) first, please. Focus on [What topics can I ask about here](http://stackoverflow.com/help/on-topic), [What types of questions should I avoid asking?](http://stackoverflow.com/help/dont-ask), [How to ask a good question](http://stackoverflow.com/help/how-to-ask), [How to create a Minimal, Complete, and Verifiable example](http://stackoverflow.com/help/mcve) and [Stack Overflow question checklist](http://meta.stackoverflow.com/questions/260648/stack-overflow-question-checklist). – David Ferenczy Rogožan Apr 20 '17 at 15:39

1 Answers1

1

Origin-centered ellipse, rotated by angle Theta, has equations

x = a * Cos(t) * Cos(theta) - b * Sin(t) * Sin(theta) 
y = a * Cos(t) * Sin(theta) + b * Sin(t) * Cos(theta)

We can introduce pseudoangle Fi and magnitude M

 Fi = atan2(a * Sin(theta), b * Cos(Theta))
 M = Sqrt((a * Sin(theta))^2 + (b * Cos(Theta))^2)

so

 y = M * Sin(Fi) * Cos(t) + M * Cos(Fi) * Sin(t)
 y/M = Sin(Fi) * Cos(t) +  Cos(Fi) * Sin(t)
 y/M = Sin(Fi + t) 

 Fi + t = ArcSin( y / M)
 Fi + t = Pi - ArcSin( y / M)
 t1 = ArcSin( y / M) - Fi        //note two values
 t2 = Pi - ArcSin( y / M) - Fi

Now substitute both values of t in the first equation and get values of X for given Y

If you have general ellipse equation like

 A*x^2 + 2*B*x*y + C*y^2 + D*x + E*y + F = 0

just substitute y by known value ans solve quadratic equation for x

MBo
  • 77,366
  • 5
  • 53
  • 86