Fit bipolar sigmoid python

Question

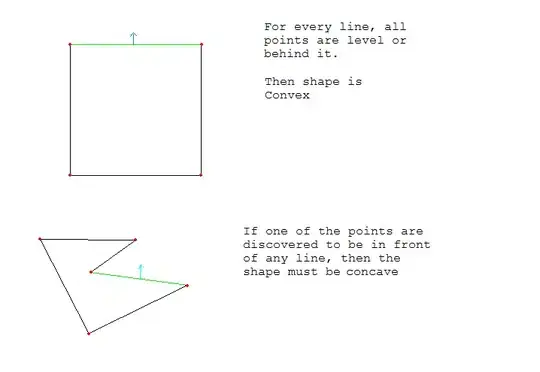
I'm stuck trying to fit a bipolar sigmoid curve - I'd like to have the following curve:

but I need it shifted and stretched. I have the following inputs:

x[0] = 8, x[48] = 2

So over 48 periods I need to drop from 8 to 2 using a bipolar sigmoid function to approximate a nice smooth dropoff. Any ideas how I could derive the curve that would fit those parameters?

Here's what I have so far, but I need to change the sigmoid function:

import math

def sigmoid(x):
  return 1 / (1 + math.exp(-x))


plt.plot([sigmoid(float(z)) for z in range(1,48)])

`atan` and `atanh` are popular sigmoid functions – f5r5e5d Apr 04 '17 at 17:16 — f5r5e5d, Apr 04 '17 at 17:16

score 3 · Answer 1 · answered Apr 04 '17 at 17:16

You could redefine the sigmoid function like so

def sigmoid(x, a, b, c, d):
    """ General sigmoid function
    a adjusts amplitude
    b adjusts y offset
    c adjusts x offset
    d adjusts slope """
    y = ((a-b) / (1 + np.exp(x-(c/2))**d)) + b
    return y

x = np.arange(49)
y = sigmoid(x, 8, 2, 48, 0.3)

plt.plot(x, y)

Severin's answer is likely more robust, but this should be fine if all you want is a quick and dirty solution.

In [2]: y[0]
Out[2]: 7.9955238269969806

In [3]: y[48]
Out[3]: 2.0044761730030203

score 1 · Accepted Answer · edited May 23 '17 at 12:17

From generic bipolar sigmoid function:

f(x,m,b)= 2/(1+exp(-b*(x-m))) - 1

there are two parameters and two unknowns - shift m and scale b

You have two condition:f(0) = 8, f(48) = 2

take first condition, express b vs m, together with second condition write non-linear function to solve, and then use fsolve from SciPy to solve it numerically, and recover back b and m.

Here related by similar method question and answer: How to random sample lognormal data in Python using the inverse CDF and specify target percentiles?

Cleb · Answer 3 · 2017-04-04T18:50:31.300

Alternatively, you could also use curve_fit which might come in handy if you have more than just two datapoints. The output looks like this:

As you can see, the graph contains the desired data points. I used @lanery's function for the fit; you can of course choose any function you like. This is the code with some inline comments:

import numpy as np
import matplotlib.pyplot as plt
from scipy.optimize import curve_fit

def sigmoid(x, a, b, c, d):
    return ((a - b) / (1. + np.exp(x - (c / 2)) ** d)) + b

# one needs at least as many data points as parameters, so I just duplicate the data
xdata = [0., 48.] * 2
ydata = [8., 2.] * 2

# plot data
plt.plot(xdata, ydata, 'bo', label='data')

# fit the data
popt, pcov = curve_fit(sigmoid, xdata, ydata, p0=[1., 1., 50., 0.5])

# plot the result
xdata_new = np.linspace(0, 50, 100)
plt.plot(xdata_new, sigmoid(xdata_new, *popt), 'r-', label='fit')
plt.legend(loc='best')
plt.show()

Fit bipolar sigmoid python

3 Answers3