One way would be to use the Cholesky factorisation. I use the upper triangular form below, so that
M = U'*U
where ' is adjoint and U is upper triangular.
Note that det(M) = square( |det(U)|) and that the determinant of U is the product of its diagonal elements.
We can compute the factor of a matrix obtained from M by appending a row and column like this:
M~ = ( M n )
( n' p )
U~ = ( U x )
( 0 y )
where
U'*x = n
y = sqrt( p - x'*x)
and so det( M~) = det( M) * ( p - x'*x)
I'm not sure of the best way to use this. There is quite a neat recursive way: in pseudo C code
void det_step( double* U, double det, int high_ix)
{
int ix;
for( ix=high_ix+1; ix<dim; ++ix)
{ // notionally add row, col ix
// augment U, update det (and store in the output)
det_step( U, det, ix);
}
}
void dets( double* M, int dim)
{
int ix;
for( ix=0; ix<dim; ++ix)
{ // compute U and det for matrix consisting of just row/col ix
// store det in the output
det_step( U, det, ix);
}
}
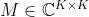 and
and 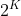 square submatrices of
square submatrices of 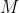 ,
,  defined:
defined: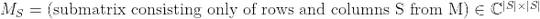
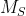 .
.