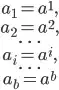Let me start by stating that while my question is of a programming nature, the part where I get stuck is a bit mathematical. So I'm not sure if this is the correct place to post about it, but I wasn't sure where else.
I'm trying to define some boolean function that returns true if a point (x,y) is inside a certain shape and false if outside. To clarify that, the following code would work for defining an annulus (a ring) of inner radius r1 and outer radius r2:
def ring(pos):
(x, y) = pos
rsq = x ** 2 + y ** 2
return (r1 ** 2 < rsq < r2 ** 2)
My question would be if someone could help me come up with a clever way to define a function like this for a hexagonal region. Specifically, I'd like to define a hexagonal region with side length s (which is half of the diameter), centered around the origin. Ideally it would also be oriented such that the top and bottom are sides, paralel with the x-axis.