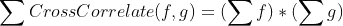Testing similarity of several datasets by producing a cross-correlation matrix

Question

I am trying to compare several datasets and basically test, if they show the same feature, although this feature might be shifted, reversed or attenuated. A very simple example below:

A = np.array([0., 0, 0, 1., 2., 3., 4., 3, 2, 1, 0, 0, 0])
B = np.array([0., 0, 0, 0, 0, 1, 2., 3., 4, 3, 2, 1, 0])
C = np.array([0., 0, 0, 1, 1.5, 2, 1.5, 1, 0, 0, 0, 0, 0])
D = np.array([0., 0, 0, 0, 0, -2, -4, -2, 0, 0, 0, 0, 0])
x = np.arange(0,len(A),1)

I thought the best way to do it would be to normalize these signals and get absolute values (their attenuation is not important for me at this stage, I am interested in the position... but I might be wrong, so I will welcome thoughts about this concept too) and calculate the area where they overlap. I am following up on this answer - the solution looked very elegant and simple, but I may be implementing it wrongly.

def normalize(sig):
    #ns = sig/max(np.abs(sig))
    ns = sig/sum(sig)
    return ns
a = normalize(A)
b = normalize(B)
c = normalize(C)
d = normalize(D)

which then look like this:

But then, when I try to implement the solution from the answer, I run into problems.

OLD

for c1,w1 in enumerate([a,b,c,d]):
    for c2,w2 in enumerate([a,b,c,d]):
        w1 = np.abs(w1)
        w2 = np.abs(w2)
        M[c1,c2] = integrate.trapz(min(np.abs(w2).any(),np.abs(w1).any()))
print M

Produces TypeError: 'numpy.bool_' object is not iterable or IndexError: list assignment index out of range. But I only included the .any() because without them, I was getting the ValueError: The truth value of an array with more than one element is ambiguous. Use a.any() or a.all().

EDIT - NEW (thanks @Kody King)

The new code is now:

M = np.zeros([4,4])
SH = np.zeros([4,4])
for c1,w1 in enumerate([a,b,c,d]):
    for c2,w2 in enumerate([a,b,c,d]):
        crossCorrelation = np.correlate(w1,w2, 'full')
        bestShift = np.argmax(crossCorrelation)

        # This reverses the effect of the padding.
        actualShift = bestShift - len(w2) + 1
        similarity = crossCorrelation[bestShift]

        M[c1,c2] = similarity
        SH[c1,c2] = actualShift
M = M/M.max()
print M, '\n', SH

And the output:

[[ 1.          1.          0.95454545  0.63636364]
 [ 1.          1.          0.95454545  0.63636364]
 [ 0.95454545  0.95454545  0.95454545  0.63636364]
 [ 0.63636364  0.63636364  0.63636364  0.54545455]] 
[[ 0. -2.  1.  0.]
 [ 2.  0.  3.  2.]
 [-1. -3.  0. -1.]
 [ 0. -2.  1.  0.]]

The matrix of shifts looks ok now, but the actual correlation matrix does not. I am really puzzled by the fact that the lowest correlation value is for correlating d with itself. What I would like to achieve now is that:

---

EDIT - UPDATE

Following on the advice, I used the recommended normalization formula (dividing the signal by its sum), but the problem wasn't solved, just reversed. Now the correlation of d with d is 1, but all the other signals don't correlate with themselves.

New output:

[[ 0.45833333  0.45833333  0.5         0.58333333]
 [ 0.45833333  0.45833333  0.5         0.58333333]
 [ 0.5         0.5         0.57142857  0.66666667]
 [ 0.58333333  0.58333333  0.66666667  1.        ]] 
[[ 0. -2.  1.  0.]
 [ 2.  0.  3.  2.]
 [-1. -3.  0. -1.]
 [ 0. -2.  1.  0.]]

---

1. The correlation value should be highest for correlating a signal with itself (i.e. to have the highest values on the main diagonal).
2. To get the correlation values in the range between 0 and 1, so as a result, I would have 1s on the main diagonal and other numbers (0.x) elsewhere.

I was hoping the M = M/M.max() would do the job, but only if condition no. 1 is fulfilled, which it currently isn't.

Answer 1

As ssm said numpy's correlate function works well for this problem. You mentioned that you are interested in the position. The correlate function can also help you tell how far one sequence is shifted from another.

import numpy as np

def compare(a, b):
    # 'full' pads the sequences with 0's so they are correlated
    # with as little as 1 actual element overlapping.
    crossCorrelation = np.correlate(a,b, 'full')
    bestShift = np.argmax(crossCorrelation)

    # This reverses the effect of the padding.
    actualShift = bestShift - len(b) + 1
    similarity = crossCorrelation[bestShift]

    print('Shift: ' + str(actualShift))
    print('Similatiy: ' + str(similarity))
    return {'shift': actualShift, 'similarity': similarity}

print('\nExpected shift: 0')
compare([0,0,1,0,0], [0,0,1,0,0])
print('\nExpected shift: 2')
compare([0,0,1,0,0], [1,0,0,0,0])
print('\nExpected shift: -2')
compare([1,0,0,0,0], [0,0,1,0,0])

Edit:

You need to normalize each sequence before correlating them, or the larger sequences will have a very high correlation with the all the other sequences.

A property of cross-correlation is that:

So if you normalize by dividing each sequence by it's sum, the similarity will always be between 0 and 1.

I recommend you don't take the absolute value of a sequence. That changes the shape, not just the scale. For instance np.abs([1, -2]) == [1, 2]. Normalizing will already ensure that sequence is mostly positive and adds up to 1.

Second Edit:

I had a realization. Think of the signals as vectors. Normalized vectors always have a max dot product with themselves. Cross-Correlation is just a dot product calculated at various shifts. If you normalize the signals like you would a vector (divide s by sqrt(s dot s)), the self correlations will always be maximal and 1.

import numpy as np

def normalize(s):
    magSquared = np.correlate(s, s) # s dot itself
    return s / np.sqrt(magSquared)

a = np.array([0., 0, 0, 1., 2., 3., 4., 3, 2, 1, 0, 0, 0])
b = np.array([0., 0, 0, 0, 0, 1, 2., 3., 4, 3, 2, 1, 0])
c = np.array([0., 0, 0, 1, 1.5, 2, 1.5, 1, 0, 0, 0, 0, 0])
d = np.array([0., 0, 0, 0, 0, -2, -4, -2, 0, 0, 0, 0, 0])

a = normalize(a)
b = normalize(b)
c = normalize(c)
d = normalize(d)

M = np.zeros([4,4])
SH = np.zeros([4,4])
for c1,w1 in enumerate([a,b,c,d]):
    for c2,w2 in enumerate([a,b,c,d]):
        # Taking the absolute value catches signals which are flipped.
        crossCorrelation = np.abs(np.correlate(w1, w2, 'full'))
        bestShift = np.argmax(crossCorrelation)

        # This reverses the effect of the padding.
        actualShift = bestShift - len(w2) + 1
        similarity = crossCorrelation[bestShift]

        M[c1,c2] = similarity
        SH[c1,c2] = actualShift
print(M, '\n', SH)

Outputs:

[[ 1.          1.          0.97700842  0.86164044]
[ 1.          1.          0.97700842  0.86164044]
[ 0.97700842  0.97700842  1.          0.8819171 ]
[ 0.86164044  0.86164044  0.8819171   1.        ]]
[[ 0. -2.  1.  0.]
[ 2.  0.  3.  2.]
[-1. -3.  0. -1.]
[ 0. -2.  1.  0.]]

Answer 2

You want to use a cross-correlation between the vectors:

• https://en.wikipedia.org/wiki/Cross-correlation
• https://docs.scipy.org/doc/numpy/reference/generated/numpy.correlate.html

For example:

>>> np.correlate(A,B)
array([ 31.])

>>> np.correlate(A,C)
array([ 19.])

>>> np.correlate(A,D)
array([-28.])

If you don't care about the sign, you can simply take the absolute value ...