0

I have the following ordinary least squares model (OLS) interactive model that I want to extract discrete marginal effects (i.e. the average marginal effect of weight across discrete categories of speed and foreign-build autos) for the triple interactionweight* speed*foreign:

mpg ~ cost + foreign + weight + speed + foreign + cost*foreign + weight*speed + weight*speed*foreign

As one can see, there are three interactions in the model. The variables are specified as follows:

cost is a continuous variable centered at the mean value of all cars on the market, with negative values indicating degrees below the mean and positive values indicating more expensive cars.

foreign is a binary variable, 1 foreign/0 domestic

weight is a continuous variable

speed is a factor variable indicating how fast the car goes in three categories, low-medium-high. Low is the base-line category (omitted category).

The quantity of interest is the triple interaction in the model: weight*speed*foreign. I use the following code to estimate the model and extract the relevant coefficients and variance covariance matrix. I want to use the following procedure from Berry et al. (2016) article: "Improving Tests of Theories Positing Interaction", using the following chart:Marginal Effects Formulation

I extract the relevant coefficients needed to derive the marginal effects and the variance-covariance matrix using the following code:

m <- lm(mpg ~ cost + foreign + weight + speed + foreign + cost*foreign + weight*speed + weight*speed*foreign, data=x)
beta.hat <- coef(m) 
cov <-  vcov(m)

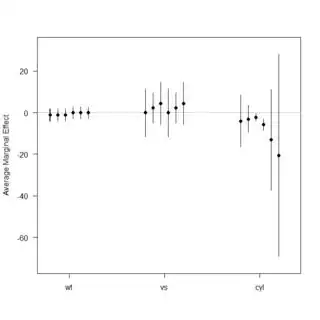
Ultimately, I want a data frame containing the average marginal effect of weight across the different discrete categories of speed & foreign, with the end goal being a dot-plot showing discrete marginal effects. Following the image, I know how to derive the marginal effects for the two non-omitted categories of the factor variable (speed). For example, I think this is done correctly for the "high" speed":

z0 <- seq(0,1,1) #This captures the two-categories of the Z conditioning variable of foreign
dy.dx <-  beta.hat["weight"] + beta.hat["weight*speed=High"] + beta.hat["weight*foreign*speed=High"]*z0 # Discrete Marginal Effect
se.dy.dx <- sqrt(cov["weight", "weight"] + z0^2*cov["weight * speed=High", "weight * speed=High"] + z0^2*cov["foreign * weight", "foreign * weight"] + z0^2*z0^2*cov["foreign * weight * speed=High", "foreign * weight * speed=High"] + 2*z0*cov["weight","weight * speed=High"] + 2*z0*cov["weight","foreign * weight"] + 2*z0*z0*cov["weight","foreign * weight * speed=High"] + 2*z0*z0*cov["weight * speed=High","foreign * weight"] + 2*z0*z0^2*cov["weight * speed=High","foreign * weight * speed=High"] + 2*z0*z0^2*cov["foreign * weight","foreign * weight * speed=High"]) #Compute Standard Errors for MEs of foreign and domestic cars

The main question I have is how do I derive the average marginal effects of weight for the omitted category of speed? I understand that this is captured by the weight*speed constituent term, but do I need to consider the triple interaction in calculating the standard errors, dy.dx of the estimates? Is this an adequate solution given Berry et al.'s table in row 3?

jay.sf
  • 60,139
  • 8
  • 53
  • 110
Joe Maj
  • 1
  • 3

1 Answers1

1

I'm not sure what dataset you're using, so I'll present a slightly modified version using the built-in mtcars dataset. To get at the quantities you want, I'll use the margins package

# three variables
## wt # continuous (your `weight` variable)
## vs # 0/1 (your `foreign` variable)
## cyl # categorical (your `speed` variable)

# note simplified formula construction:
m <- lm(mpg ~ wt*vs*cyl, data = mtcars)

library("margins")
(mar <- margins(m, at=list(vs = 0:1, cyl = c(4,6,8))))
Average marginal effects at specified values
## lm(formula = mpg ~ wt * vs * cyl, data = mtcars)
## 
##  at(vs) at(cyl)      wt      vs      cyl
##       0       4  -4.083 -0.0502 -1.18447
##       1       4  -5.721 -0.0502 -0.05289
##       0       6  -3.129  2.2130 -1.18447
##       1       6 -13.139  2.2130 -0.05289
##       0       8  -2.176  4.4761 -1.18447
##       1       8 -20.557  4.4761 -0.05289

The wt column in the above shows the marginal effect of the continuous term across levels of the two variables it is interacted with. To plot this you have a couple of options. One simple one is just:

plot(mar)

marginsplot

To get a glance at the result. Another might be to take the summary() object (which is just a data frame) and plot however you want (base, ggplot, etc.):

summary(mar)
##  factor vs cyl      AME      SE       z      p    lower   upper
##     cyl  0   4  -1.1845  1.5304 -0.7740 0.4389  -4.1839  1.8150
##     cyl  0   6  -1.1845  1.5304 -0.7740 0.4389  -4.1839  1.8150
##     cyl  0   8  -1.1845  1.5304 -0.7740 0.4389  -4.1839  1.8150
##     cyl  1   4  -0.0529  1.4410 -0.0367 0.9707  -2.8772  2.7714
##     cyl  1   6  -0.0529  1.4398 -0.0367 0.9707  -2.8748  2.7690
##     cyl  1   8  -0.0529  1.4405 -0.0367 0.9707  -2.8761  2.7703
##      vs  0   4  -0.0502  5.8858 -0.0085 0.9932 -11.5861 11.4857
##      vs  0   6   2.2130  3.6550  0.6055 0.5449  -4.9508  9.3767
##      vs  0   8   4.4761  5.2348  0.8551 0.3925  -5.7839 14.7361
##      vs  1   4  -0.0502  5.8896 -0.0085 0.9932 -11.5936 11.4932
##      vs  1   6   2.2130  3.6611  0.6045 0.5455  -4.9626  9.3886
##      vs  1   8   4.4761  5.2397  0.8543 0.3930  -5.7935 14.7457
##      wt  0   4  -4.0826  6.3551 -0.6424 0.5206 -16.5383  8.3731
##      wt  0   6  -3.1291  3.3271 -0.9405 0.3470  -9.6502  3.3920
##      wt  0   8  -2.1756  0.9056 -2.4023 0.0163  -3.9507 -0.4006
##      wt  1   4  -5.7210  1.3883 -4.1209 0.0000  -8.4420 -3.0000
##      wt  1   6 -13.1390 12.3771 -1.0616 0.2884 -37.3977 11.1198
##      wt  1   8 -20.5569 24.7939 -0.8291 0.4070 -69.1522 28.0383
Thomas
  • 43,637
  • 12
  • 109
  • 140