I am trying to understand the Nauty algorithm.
Following this article: http://www.math.unl.edu/~aradcliffe1/Papers/Canonical.pdf
In this algorithm the vertices are distinguished based on their degree and the relative degree of a group corresponding to other groups(group action). In this way we get the groups as:
1379|2468|5
After this step, splitting is done as mentioned in this paper - page 7.
One image from this article is:
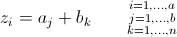
I am unable to understand how the splitting is done from
1379|2468|5 to 1|9|37|68|24|5
Why 1 and 9 went to different groups and 37 went to another group.