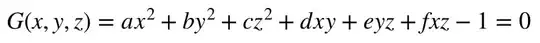probability of each terminal node in a directed graph

Question

I have a directed graph G(V,E) and weight w(u,v).

In this graph weight w(u,v) represents how many times the node(v) has visited from node(u). for example(See this for a directed graph image):

     1        3
  A ----- B ----- D
  | \____/|
 1|   4   |2
  |       |
  C       E

As C and B are visited once from A, D is visited 3 times from B and so on. Given this data how can I calculate exact probability to reach each terminal node i.e; C,E,D, if starting from A.

Any suggestion?

You can first estimate the probability that you will go from `node(i)` to `node(j)`. For instance, you could say that the probability of going from `B` to `A` is 4/(4+2+3) = 4/9. You put this in a matrix that's all zeros, except for the nodes that are directly connected in your graph. That's a Markov chain. Now you can simulate. Search about Markov processes in http://stats.stackexchange.com/, there should be something helpful there. — giusti, Feb 24 '17 at 18:51

score 6 · Accepted Answer · answered Feb 24 '17 at 21:22

The following are the un-normalized and then row-normalized transition matrices of the markov chain, also shown in the figure. We need to calculate the absorption probabilities as shown in the figure.

  A B C D E
A 0 1 1 0 0
B 4 0 0 3 2
C 0 0 0 0 0
D 0 0 0 0 0
E 0 0 0 0 0  

          A   B   C         D         E
A 0.0000000 0.5 0.5 0.0000000 0.0000000
B 0.4444444 0.0 0.0 0.3333333 0.2222222
C 0.0000000 0.0 0.0 0.0000000 0.0000000
D 0.0000000 0.0 0.0 0.0000000 0.0000000
E 0.0000000 0.0 0.0 0.0000000 0.0000000

score 0 · Answer 2 · answered Feb 24 '17 at 19:53

Let pXY be the probability you end up in terminal state Y if you start in state X.

You want to calculate pAC, pAD, pAE, pBC, pBD, pBE.

For example, to calculate pAC you have two equations:

pAC = 1/2 + 1/2 pBC
pBC = 4/9 pAC

That is, the probability you end in C starting from A is 1/2 (when you move there directly), and 1/2 of the probability that you end up in C if you move first to B. And if you start at B, the probability that you end up in C is if you first move to A and from there end up in C.

Substituting the second into the first gives you:

pAC = 1/2 + 1/2 * 4/9 pAC
pAC(1 - 2/9) = 1/2
pAC = 9/14

This immediately gives you pBC = 4/14 = 2/7.

The other 4 probabilities can be computed in the same way.

probability of each terminal node in a directed graph

2 Answers2